题目内容
如图,在直角梯形ABEF中, ,
,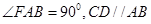 ,讲DCEF沿CD折起,使得
,讲DCEF沿CD折起,使得 ,得到一个几何体,
,得到一个几何体,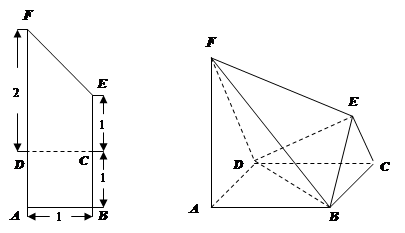
(1)求证: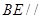 平面ADF;
平面ADF;
(2)求证:AF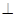 平面ABCD;
平面ABCD;
(3)求三棱锥E-BCD的体积.
(1)见解析(2)见解析(3)
解析试题分析:
(1)要证明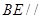 平面ADF,可以通过BCE面与ADF面平行来得到线面平行,在折叠过程中,会保持BC//AD,CE//DF,故两平面内两条相交的直线相互平行,故可以证明BCE面与ADF面平行来得到线面平行
平面ADF,可以通过BCE面与ADF面平行来得到线面平行,在折叠过程中,会保持BC//AD,CE//DF,故两平面内两条相交的直线相互平行,故可以证明BCE面与ADF面平行来得到线面平行
(2)要证明AF垂直于ABCD面,只需要证明AF与ABCD面内两条相交的直线AD与DC垂直即可,利用三角形ADF的正弦定理,可以求出AF长度,加以勾股定理就可以证明AF与AD垂直,DC垂直于DF和AD,所以DC垂直于面AFD,进而也是垂直于AF的.
(3)求三棱锥E-BCD的体积,由(1)(2)可以知道面BCE与面ADF平行且DC垂直于面ADF,进而有DC垂直于面BCE,所以求三棱锥的体积可以以三角形BCE底面,DC为高,则高长度已知,底面三角形面积可以利用EC,BC及其两边夹角的正弦值来求的.
试题解析:
(1)由已知条件可知 ,折叠之后平行关系不变,又因为
,折叠之后平行关系不变,又因为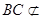 平面
平面 ,
, 平面
平面 ,所以
,所以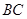 //平面
//平面 ;
;
同理 //平面
//平面 . 2分
. 2分
又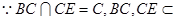 平面
平面 ,
, 平面
平面 //平面
//平面 .
.
又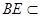 平面
平面 ,
,
∴ //平面
//平面 . 4分
. 4分
(2)由于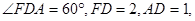
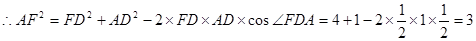 ,即
,即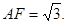
 . 6分
. 6分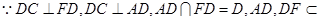 平面
平面 ,
,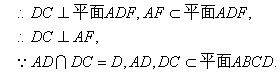
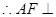 平面
平面 . 8分
. 8分
(3)法一: 平面
平面 ,
,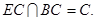
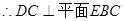 . 10分
. 10分
又 ,
,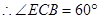 .
.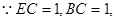
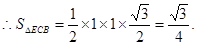 12分
12分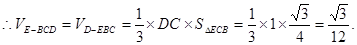 14分
14分
法二:取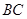 中点
中点 ,连接
,连接 .
.
由(2)易知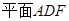 ⊥平面
⊥平面 ,又平面
,又平面 //平面
//平面 ,
,
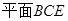 ⊥平面
⊥平面 . 10分
. 10分
又 ,
,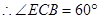 .
.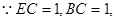
 ,
,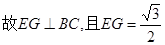 , 12分
, 12分 .
. . 14分
. 14分
考点:线面平行面面平行线面垂直三棱锥体积

练习册系列答案
相关题目
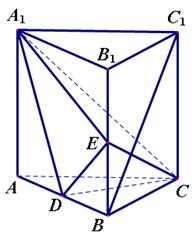
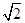 ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积. 中,已知
中,已知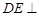 平面
平面 ,
,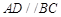 ,
,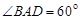 ,
,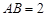 ,
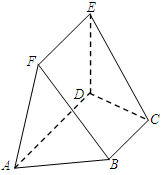
,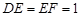 .
.
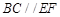 ;
;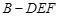 的体积.
的体积.
 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.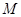 是母线
是母线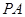 的中点,
的中点,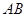 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线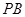 所成的角的大小等于
所成的角的大小等于 .
.
 与
与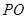 所成的角;
所成的角; ,
,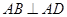 ,
,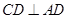 ,
,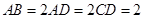 沿
沿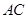 折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积
折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积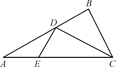 图①
图①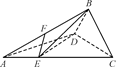 图②
图②