题目内容
在△ABC中,BC=24,AB+AC=26,则△ABC面积的最大值是
- A.24
- B.65
- C.60
- D.30
C
分析:本题是研究三角形面积最大值的问题,由于已知三边的和,故可以借助海伦公式建立面积关于边的函数,再利用基本不等式求最值
解答:由题意,三角形的周长是50,由令AB=x,则BC=26-x
由海伦公式可得三角形的面积
S=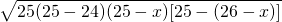 =5
=5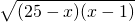 ≤5×
≤5×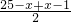 =60
=60
等号仅当25-x=x-1即x=13时成立
故三角形的面积的最大值是60
故选C
点评:本题考查三角形中的几何计算,解题的关键是建立起面积的函数模型,根据其形式选择求最值的方法,利用海伦公式求面积适合三边已知的情况,比较快捷.
分析:本题是研究三角形面积最大值的问题,由于已知三边的和,故可以借助海伦公式建立面积关于边的函数,再利用基本不等式求最值
解答:由题意,三角形的周长是50,由令AB=x,则BC=26-x
由海伦公式可得三角形的面积
S=
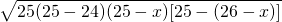 =5
=5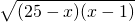 ≤5×
≤5×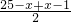 =60
=60等号仅当25-x=x-1即x=13时成立
故三角形的面积的最大值是60
故选C
点评:本题考查三角形中的几何计算,解题的关键是建立起面积的函数模型,根据其形式选择求最值的方法,利用海伦公式求面积适合三边已知的情况,比较快捷.

练习册系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |