题目内容
已知函数 ,
, ,其中
,其中 为常数,
为常数, ,函数
,函数 和
和 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为 、
、 ,且
,且 .
.
(1)求常数 的值及
的值及 、
、 的方程;
的方程;
(2)求证:对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有 ;
;
(3)若存在 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,
, ,其中
,其中 为常数,
为常数, ,函数
,函数 和
和 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为 、
、 ,且
,且 .
.(1)求常数
 的值及
的值及 、
、 的方程;
的方程;(2)求证:对于函数
 和
和 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有 ;
;(3)若存在
 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1) ,所以直线
,所以直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ;
;
(2)详见解析;(3)实数 的取值范围是
的取值范围是 .
.
 ,所以直线
,所以直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ;
;(2)详见解析;(3)实数
 的取值范围是
的取值范围是 .
.试题分析:(1)先确定函数
 、
、 的图象与坐标轴的交点,利用相应的图象在交点处的切线平行列出有关
的图象与坐标轴的交点,利用相应的图象在交点处的切线平行列出有关 的方程求解出
的方程求解出 的值,然后在确定两个函数图象与坐标轴的交点,利用导数求出直线
的值,然后在确定两个函数图象与坐标轴的交点,利用导数求出直线 、
、 的方程;
的方程;(2)利用
 的性质,引入函数
的性质,引入函数 ,从而将
,从而将 化为
化为
 ,构造新函数
,构造新函数 ,
, ,问题转换为
,问题转换为
 进行处理;(3)将等价转化为
进行处理;(3)将等价转化为 ,构造新函数
,构造新函数 ,将问题转化为
,将问题转化为 进行处理,结合导数来求函数
进行处理,结合导数来求函数 的最小值,在判断导数的符号时,可以结合基本不等式来处理.
的最小值,在判断导数的符号时,可以结合基本不等式来处理.试题解析:(1)对于函数
 而言,
而言, ,函数
,函数 的定义域为
的定义域为 ,
,故函数
 与
与 轴无交点,因此函数
轴无交点,因此函数 与
与 轴有交点,
轴有交点,令
 ,解得
,解得 ,
, ,
,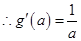 ,
, ,
, ,即函数
,即函数 的图象与
的图象与 轴无交点,与
轴无交点,与 轴有交点,
轴有交点,且
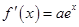 ,
, ,
,由题意知,
 ,即
,即 ,解得
,解得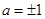 ,因为
,因为 ,所以
,所以 ,
, ,
, ,
, ,
, ,
, ,
, ,
,所以直线
 的方程为
的方程为 ,即
,即 ,
,直线
 的方程为
的方程为 ,即
,即 ;
;(2)函数
 与
与 的公共定义域为
的公共定义域为 ,
,在同一坐标系中画出函数
 ,
, 和函数
和函数 的图象,易知当
的图象,易知当 时,
时, ,
, ,
,令
 ,
, ,其中
,其中 ,
, ,故函数
,故函数 在
在 上单调递增,所以
上单调递增,所以 ,
, ,令
,令 ,解得
,解得 ,
,当
 时,
时, ,当
,当 时,
时,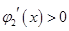 ,
,故函数
 在
在 处取得极小值,亦即最小值,即
处取得极小值,亦即最小值,即 ,
, ,
, ,证毕!
,证毕!(3)问题等价于“存在
 使得
使得 成立”
成立” “存在
“存在 使得
使得 成立”,其中
成立”,其中 ,
, 令
 ,则有
,则有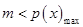 ,则函数
,则函数 的定义域为
的定义域为 ,
,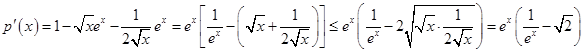
 ,故函数
,故函数 在
在 上单调递减,所以
上单调递减,所以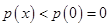 ,
,因此
 ,故实数
,故实数 的取值范围是
的取值范围是 .
.
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 .
.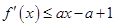 恒成立,求实数a的集合.
恒成立,求实数a的集合. .
. 的单调区间;
的单调区间; 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; (
( 是自然对数的底数)使
是自然对数的底数)使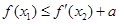 ,求实数
,求实数 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数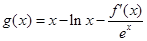 的最小值为1,其中
的最小值为1,其中 是函数f(x)的导数.
是函数f(x)的导数.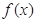 =
=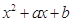 ,
,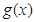 =
=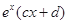 ,若曲线
,若曲线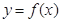 和曲线
和曲线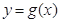 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线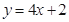 .
.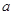 ,
,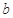 ,
, ,
, 的值;
的值; ≥-2时,
≥-2时, ≤
≤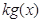 ,求
,求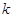 的取值范围.
的取值范围.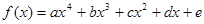 ,
,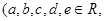 且
且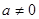 )的四个零点构成公差为2的等差数列,则
)的四个零点构成公差为2的等差数列,则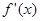 的所有零点中最大值与最小值之差是( )
的所有零点中最大值与最小值之差是( )


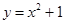 在点
在点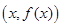 处的切线的斜率为
处的切线的斜率为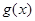 ,则函数
,则函数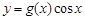 的部分图象可以为( )
的部分图象可以为( )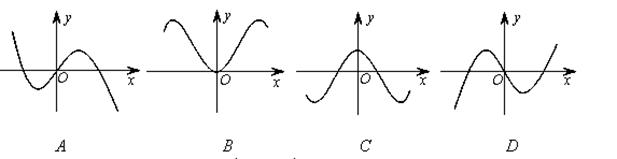
 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 =
= ,则称
,则称 是
是 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤
 ,其中
,其中 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )


