题目内容
下列说法中:
①若函数f(x)=ax2+(2a+b)x+2(x∈[2a-1,a+4])是偶函数,则实数b=2;
②f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;
③已知函数f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),则f(x)是奇函数;
④设lg2=a,lg3=b那么可以得到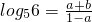 ;
;
⑤函数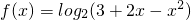 的值域是(0,2),其中正确说法的序号是________(注:把你认为是正确的序号都填上).
的值域是(0,2),其中正确说法的序号是________(注:把你认为是正确的序号都填上).
①③④
分析:利用二次函数的图象与性质,可得①是真命题;利用分段函数的单调性与图象,可得②是假命题;利用赋值法,进行验证可得③是真命题;根据对数的运算法则与换底公式,可得④是真命题;利用二次函数和对数函数的单调性,结合复合函数的单调可得⑤是真命题.由此得到正确答案.
解答:对于①,∵f(x)=ax2+(2a+b)x+2是二次函数,且图象关于直线x= 对称,
对称,
∴2a-1+a+4=0且 =0,解之得a=-1,b=2,故①正确;
=0,解之得a=-1,b=2,故①正确;
对于②,f(x)= ,
,
可得当x∈(∞,0)时,函数f(x)为增函数;当x∈(0,3)时,函数f(x)为减函数;
当x∈(3,+∞)时,函数f(x)为减函数
∴当x=0时,函数f(x)的最大值为f(0)=2,故②不正确;
对于③,对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),取x=y=1,得f(1)=f(1)+f(1),所以f(1)=0
再取x=y=-1,得f(1)=-f(-1)-f(-1)=0,所以f(-1)=0,
最后取y=-1,得f(-x)=xf(-1)-f(x),所以f(-x)=-f(x),所以f(x)是奇函数.故③正确;
对于④,lg2=a,lg3=b,则log56=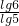 =
=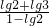 =
=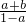 ,故④正确;
,故④正确;
对于⑤,因为0<3+2x-x2=-(x-1)2+4≤4,
所以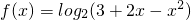 ≤log24=2,故函数函数
≤log24=2,故函数函数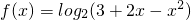 的值域是(-∞,2),故⑤不正确.
的值域是(-∞,2),故⑤不正确.
故答案为:①③④
点评:本题以命题真假的判断为载体,着重考查了函数的单调性与奇偶性、对数的运算法则、复合函数的值域和抽象函数等知识点,属于基础題.
分析:利用二次函数的图象与性质,可得①是真命题;利用分段函数的单调性与图象,可得②是假命题;利用赋值法,进行验证可得③是真命题;根据对数的运算法则与换底公式,可得④是真命题;利用二次函数和对数函数的单调性,结合复合函数的单调可得⑤是真命题.由此得到正确答案.
解答:对于①,∵f(x)=ax2+(2a+b)x+2是二次函数,且图象关于直线x=
 对称,
对称,∴2a-1+a+4=0且
 =0,解之得a=-1,b=2,故①正确;
=0,解之得a=-1,b=2,故①正确;对于②,f(x)=
 ,
,可得当x∈(∞,0)时,函数f(x)为增函数;当x∈(0,3)时,函数f(x)为减函数;
当x∈(3,+∞)时,函数f(x)为减函数
∴当x=0时,函数f(x)的最大值为f(0)=2,故②不正确;
对于③,对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),取x=y=1,得f(1)=f(1)+f(1),所以f(1)=0
再取x=y=-1,得f(1)=-f(-1)-f(-1)=0,所以f(-1)=0,
最后取y=-1,得f(-x)=xf(-1)-f(x),所以f(-x)=-f(x),所以f(x)是奇函数.故③正确;
对于④,lg2=a,lg3=b,则log56=
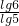 =
=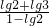 =
=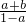 ,故④正确;
,故④正确;对于⑤,因为0<3+2x-x2=-(x-1)2+4≤4,
所以
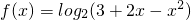 ≤log24=2,故函数函数
≤log24=2,故函数函数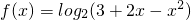 的值域是(-∞,2),故⑤不正确.
的值域是(-∞,2),故⑤不正确.故答案为:①③④
点评:本题以命题真假的判断为载体,着重考查了函数的单调性与奇偶性、对数的运算法则、复合函数的值域和抽象函数等知识点,属于基础題.

练习册系列答案
相关题目