题目内容
若关于x的方程x2-2ax+2+a=0有两个不相等的实根,求分别满足下列条件的a的取值范围.
(1)方程两根都大于1;
(2)方程一根大于1,另一根小于1.
(1)方程两根都大于1;
(2)方程一根大于1,另一根小于1.
分析:(1)构建函数f(x)=x2-2ax+2+a,结合二次函数图象,对称轴大于1,f (1)>0,△≥0,解得a 的范围即可.
(2)构建函数f(x)=x2-2ax+2+a,利用方程x2-2ax+2+a=0一个根大于1,一个根小于1,可得f(1)<0,从而可求实数a的取值范围.
(2)构建函数f(x)=x2-2ax+2+a,利用方程x2-2ax+2+a=0一个根大于1,一个根小于1,可得f(1)<0,从而可求实数a的取值范围.
解答:解:设f(x)=x2-2ax+2+a
(1)∵两根都大于1,则
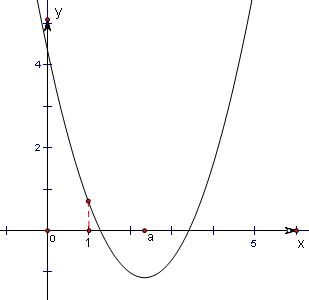
∴解得2<a<3.
(2)∵方程一根大于1,一根小于1,
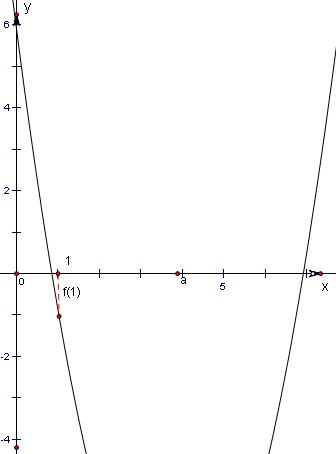
∴f(1)<0
∴1-2a+2+a<0
∴a>3.
(1)∵两根都大于1,则
|

∴解得2<a<3.
(2)∵方程一根大于1,一根小于1,

∴f(1)<0
∴1-2a+2+a<0
∴a>3.
点评:本题考查一元二次方程的根的分布与系数的关系还可用韦达定理.构建函数,建立不等式是关键.是基础题

练习册系列答案
相关题目
△ABC中三个内角为A、B、C,若关于x的方程x2-xcosAcosB-cos2
=0有一根为1,则△ABC一定是( )
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |