题目内容
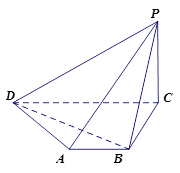
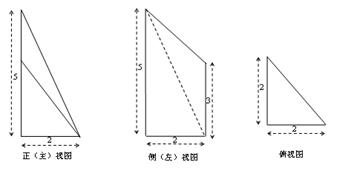
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2。

(2)若∠PDC=120°,求四棱锥P—ABCD的体积。

(2)若∠PDC=120°,求四棱锥P—ABCD的体积。
(Ⅰ)见解析 (Ⅱ)V=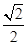
本试题主要是考查了立体几何中的面面垂直的证明和棱锥体积的计算的综合运用。
(1)因为要证明面面垂直,只要利用面面垂直的判定定理,先证明线面垂直,然后在得证。
(2)要求解棱锥的体积,关键是求解棱锥的高,借助于余弦定理和解三角形得到
解:

(Ⅰ)∵PA⊥平面ABCD,BCÌ平面ABCD,∴PA⊥BC,又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,∵BCÌ平面PBC,∴平面PBC⊥平面PAB. …4分
(Ⅱ)连结AC,则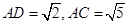 设PA=a(a>0),则
设PA=a(a>0),则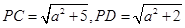
由余弦定理,cos∠PDC= …9分
…9分
解得a=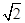 故四棱锥P—ABCD的体积V=
故四棱锥P—ABCD的体积V=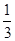 ·
·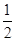 (AB+CD)·BC·PA=
(AB+CD)·BC·PA=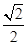
(1)因为要证明面面垂直,只要利用面面垂直的判定定理,先证明线面垂直,然后在得证。
(2)要求解棱锥的体积,关键是求解棱锥的高,借助于余弦定理和解三角形得到
解:

(Ⅰ)∵PA⊥平面ABCD,BCÌ平面ABCD,∴PA⊥BC,又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,∵BCÌ平面PBC,∴平面PBC⊥平面PAB. …4分
(Ⅱ)连结AC,则
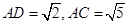 设PA=a(a>0),则
设PA=a(a>0),则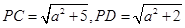
由余弦定理,cos∠PDC=
 …9分
…9分解得a=
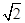 故四棱锥P—ABCD的体积V=
故四棱锥P—ABCD的体积V=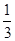 ·
·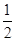 (AB+CD)·BC·PA=
(AB+CD)·BC·PA=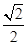

练习册系列答案
相关题目
 的体积为 .
的体积为 . 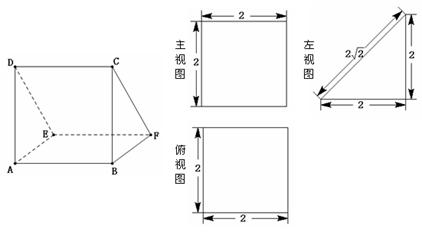
 中,已知
中,已知

 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由). ,求二面角
,求二面角 的大小.
的大小. 与
与 ,必存在平面
,必存在平面 ,使得( )
,使得( )
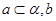 ∥
∥

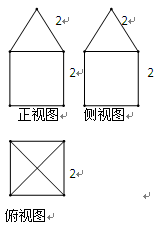
 的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )
的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为( )




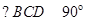 ,
,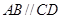 ,
,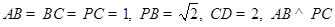 .
.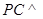 平面
平面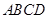 ;
;