题目内容
(本题满分13分)如图,在三棱柱 中,已知
中,已知

 侧面
侧面

(Ⅰ)求直线C1B与底面ABC所成角正切值;
(Ⅱ)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(Ⅲ)在(2)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.
 中,已知
中,已知

 侧面
侧面

(Ⅰ)求直线C1B与底面ABC所成角正切值;
(Ⅱ)在棱
 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).(Ⅲ)在(2)的条件下,若
 ,求二面角
,求二面角 的大小.
的大小.(Ⅰ) 2 (Ⅱ) 为
为 的中点
的中点 (Ⅲ) 45°
(Ⅲ) 45°
 为
为 的中点
的中点 (Ⅲ) 45°
(Ⅲ) 45°本试题主要是考查了线面角和线线垂直的证明,以及二面角的平面角的求解的综合运用。
(1)先建立空间直角坐标系,然后表示平面的法向量以及直线的斜向量,利用向量的夹角公式得到线面角的求解。
(2)假设存在点使得满足题意,然后利用垂直关系解得点的坐标,进而分析得到结论。
(3)在前面的基础上,进一步得到两个半平面的法向量的求解,结合法向量的夹角公式得到二面角的平面角的大小的运算。
解:如图,以B为原点建立空间直角坐标系,

则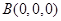 ,
, ,
, ···················· 1分
···················· 1分
(Ⅰ)直三棱柱 中,平面
中,平面 的法向量
的法向量 ,又
,又 ,
,
设 ,
,
则 ·············· 3分
·············· 3分
 即直线
即直线 与底面
与底面 所成角正切值为2. ·········· 4分
所成角正切值为2. ·········· 4分
(Ⅱ)设 ,则
,则 ,
,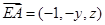
 ,∴
,∴
 ,即
,即
 ·················· 8分
·················· 8分
Ⅲ)∵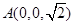 ,则
,则 ,
,
设平面 的法向量
的法向量
 ,
,
则

 ,取
,取
 ··········· 10分
··········· 10分
∵ ,
, ∴
∴ ,
,
又
 ····················· 11分
····················· 11分
∴平面 的法向量
的法向量 ,∴
,∴

∴二面角 的大小为45° 13分
的大小为45° 13分
(1)先建立空间直角坐标系,然后表示平面的法向量以及直线的斜向量,利用向量的夹角公式得到线面角的求解。
(2)假设存在点使得满足题意,然后利用垂直关系解得点的坐标,进而分析得到结论。
(3)在前面的基础上,进一步得到两个半平面的法向量的求解,结合法向量的夹角公式得到二面角的平面角的大小的运算。
解:如图,以B为原点建立空间直角坐标系,

则
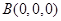 ,
, ,
, ···················· 1分
···················· 1分(Ⅰ)直三棱柱
 中,平面
中,平面 的法向量
的法向量 ,又
,又 ,
,设
 ,
,则
 ·············· 3分
·············· 3分 即直线
即直线 与底面
与底面 所成角正切值为2. ·········· 4分
所成角正切值为2. ·········· 4分(Ⅱ)设
 ,则
,则 ,
,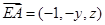
 ,∴
,∴
 ,即
,即
 ·················· 8分
·················· 8分Ⅲ)∵
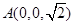 ,则
,则 ,
,设平面
 的法向量
的法向量
 ,
, 则


 ,取
,取
 ··········· 10分
··········· 10分∵
 ,
, ∴
∴ ,
,又

 ····················· 11分
····················· 11分∴平面
 的法向量
的法向量 ,∴
,∴

∴二面角
 的大小为45° 13分
的大小为45° 13分
练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目