题目内容
函数f(x)=ax3-4x+4(a∈R)在x=2取得极值,若关于x的方程f(x)=b至多有两个零点,则实数b的取值范围 .
考点:函数零点的判定定理
专题:计算题,函数的性质及应用,导数的综合应用
分析:先求导并令f′(2)=3a×4-4=0,从而求出a,再结合图象求实数b的取值范围.
解答:
解:令f′(2)=3a×4-4=0,
解得a=
,
故f(x)=
x3-4x+4,
且在x=2时有极小值f(2)=
-8+4=-
;
在x=-2时有极大值f(-2)=-
+8+4=
;
故实数b的取值范围为:(-∞,-
]∪[
,+∞).
故答案为:(-∞,-
]∪[
,+∞).
解得a=
| 1 |
| 3 |
故f(x)=
| 1 |
| 3 |
且在x=2时有极小值f(2)=
| 8 |
| 3 |
| 4 |
| 3 |
在x=-2时有极大值f(-2)=-
| 8 |
| 3 |
| 28 |
| 3 |
故实数b的取值范围为:(-∞,-
| 4 |
| 3 |
| 28 |
| 3 |
故答案为:(-∞,-
| 4 |
| 3 |
| 28 |
| 3 |
点评:本题考查了导数的应用及方程与函数的关系应用,属于中档题.

练习册系列答案
相关题目
已知
,则
的最大值为( )
|
| y-2 |
| x-3 |
| A、2 | ||
B、
| ||
| C、0 | ||
D、
|
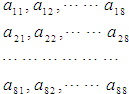 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=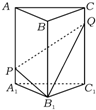 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为