题目内容
在数列{an}中,已知a1=1,且当n≥2时,a1a2…an=n2,则a3+a5等于( )A.

B.
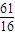
C.
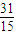
D.
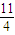
【答案】分析:首先根据题意求出a1a2…an-1=(n-1)2,与原式相除可以求出{an}的表达式,进而求出a3和a5的值.
解答:解:由题意a1a2…an=n2,
故a1a2…an-1=(n-1)2,
两式相除得:an=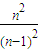 n≥2,
n≥2,
所以a3= ,a5=
,a5=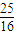 ,
,
即a3+a5=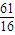 ,
,
故选B.
点评:本题主要考查数列递推式的知识点,解答本题的关键是求出数列{an}的表达式,本题比较简单.
解答:解:由题意a1a2…an=n2,
故a1a2…an-1=(n-1)2,
两式相除得:an=
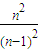 n≥2,
n≥2,所以a3=
 ,a5=
,a5=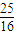 ,
,即a3+a5=
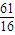 ,
,故选B.
点评:本题主要考查数列递推式的知识点,解答本题的关键是求出数列{an}的表达式,本题比较简单.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目