题目内容
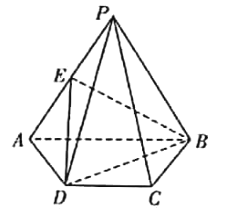
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,
,![]() 为
为![]() 的中点,现将梯形沿
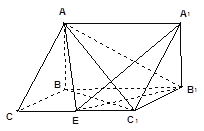
的中点,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.
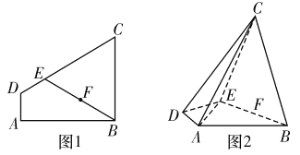
(1)求证:平面![]() 平面
平面![]() ;
;
(2)能否在线段![]() 上找到一点
上找到一点![]() (端点除外)使得直线
(端点除外)使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在点![]() 是线段
是线段![]() 的中点,使得直线
的中点,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)在直角梯形![]() 中,根据
中,根据![]() ,
,![]() ,得
,得![]() 为等边三角形,再由余弦定理求得
为等边三角形,再由余弦定理求得![]() ,满足
,满足![]() ,得到
,得到![]() ,再根据平面
,再根据平面![]() 平面
平面![]() ,利用面面垂直的性质定理证明.
,利用面面垂直的性质定理证明.
(2)建立空间直角坐标系:假设在![]() 上存在一点
上存在一点![]() 使直线
使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,且
,且![]() ,
,![]() ,求得平面
,求得平面![]() 的一个法向量,再利用线面角公式
的一个法向量,再利用线面角公式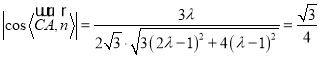 求解.
求解.
(1)证明:在直角梯形![]() 中,
中,![]() ,
,![]() ,
,
因此![]() 为等边三角形,从而
为等边三角形,从而![]() ,又
,又![]() ,
,
由余弦定理得:![]() ,
,
∴![]() ,即
,即![]() ,且折叠后
,且折叠后![]() 与
与![]() 位置关系不变,
位置关系不变,
又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)∵![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,
的中点,
∴![]() ,又∵平面
,又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,从而
,从而![]() ,以
,以![]() 为坐标原点建立如图所示的空间直角坐标系:
为坐标原点建立如图所示的空间直角坐标系:
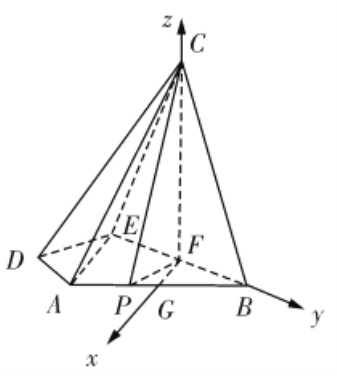
则![]() ,
, ,则
,则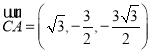 ,
,
假设在![]() 上存在一点
上存在一点![]() 使直线
使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,且
,且![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,故
,故![]() ,
,
∴ ,又
,又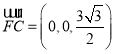 ,
,
该平面![]() 的法向量为
的法向量为![]() ,
,
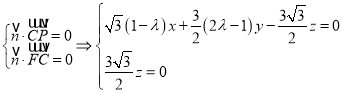 ,
,
令![]() 得
得![]() ,
,
∴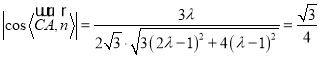 ,
,
解得![]() 或
或![]() (舍),
(舍),
综上可知,存在点![]() 是线段
是线段![]() 的中点,使得直线
的中点,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】为了迎接2019年的高考,某学校进行了第一次模拟考试,其中五个班的考试成绩在500分以上的人数如下表,![]() 为班级,
为班级,![]() 表示500分以上的人数
表示500分以上的人数
| 1 | 2 | 3 | 4 | 5 |
| 20 | 25 | 30 | 30 | 25 |
(1)若给出数据,班级![]() 与考试成绩500以上的人数
与考试成绩500以上的人数![]() ,满足回归直线方程
,满足回归直线方程![]() ,求出该回归直线方程;
,求出该回归直线方程;
(2)学校为了更好的提高学生的成绩,了解一模的考试成绩,从考试成绩在500分以上1,3班学生中,利用分层抽样抽取5人进行调研,再从选中的5人中,再选3名学生写出“经验介绍”文章,则选的三名学生1班一名,3班2名的概率.
参考公式: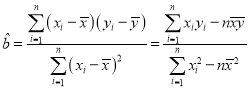 ,
,![]() .
.