题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知点是直角坐标平面内的动点,点到直线的距离为,到点的距离为,且.
(1)求动点P所在曲线C的方程;
(2)直线过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线的垂线,对应的垂足分别为,试判断点F与以线段为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记,,(A、B、是(2)中的点),问是否存在实数,使成立.若存在,求出的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线、点、曲线C:,则使等式成立的的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
解 (1) 设动点为, 1分
依据题意,有
,化简得. 3分
因此,动点P所在曲线C的方程是:. ……………………4分
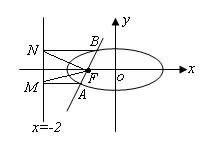 (2) 点F在以MN为直径的圆的外部.
(2) 点F在以MN为直径的圆的外部.
理由:由题意可知,当过点F的直线的斜率为0时,不合题意,故可设直线:,如图所示. 5分
联立方程组,可化为,
则点的坐标满足. 7分
又、,可得点、.
点与圆的位置关系,可以比较点到圆心的距离与半径的大小来判断,也可以计算点与直径形成的张角是锐角、直角、钝角来加以判断.
因,,则=.9分
于是,为锐角,即点F在以MN为直径的圆的外部. 10分
(3)依据(2)可算出,,
则
,
. 14分
所以,,即存在实数使得结论成立. 15分
对进一步思考问题的判断:正确. 18分

 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处