题目内容
已知点F1,F2分别为椭圆C: 的左右焦点,P是椭圆C上的一点,且
的左右焦点,P是椭圆C上的一点,且 的面积为
的面积为
(Ⅰ)求椭圆C的方程;
(Ⅱ)点M的坐标为
 ,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的
,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的 是否为定值?若是求出这个定值;若不是说明理由.
是否为定值?若是求出这个定值;若不是说明理由.
【答案】分析:(Ⅰ)设|PF1|=m,|PF2|=n,在△PF1F2中,由余弦定理以及三角形的面积,结合椭圆定义,求出a,c,b可得椭圆的方程.
(Ⅱ)利用直线与椭圆方程,通过韦达定理,结合向量的数量积化简得到定值即可.
解答:解:(Ⅰ)设|PF1|=m,|PF2|=n,在三角形PF1F2中,由余弦定理得4=m2+n2-2mncos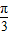 ,由三角形的面积为
,由三角形的面积为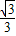
所以 ,所以mn=
,所以mn= ,所以m+n=2
,所以m+n=2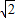 ,所以a=
,所以a=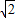 ;又c=1,所以b=1,椭圆C的方程为
;又c=1,所以b=1,椭圆C的方程为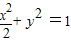 ;
;
(Ⅱ)由F2(1,0),直线l的方程为y=k(x-1).由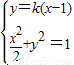 消去y,(2k2+1)x2-4k2x+2(k2-1)=0
消去y,(2k2+1)x2-4k2x+2(k2-1)=0
设A(x1,y1),B(x2,y2)则x1+x2=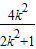 ,x1x2=
,x1x2=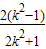
∴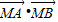 =(x1-
=(x1- ,y1)(x2-
,y1)(x2- ,y2)=(x1-
,y2)=(x1- )(x2-
)(x2- )+y1y2
)+y1y2
=(x1- )(x2-
)(x2- )+k2(x1-1)(x2-1)
)+k2(x1-1)(x2-1)
=(k2+1)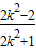 -
-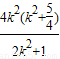 +
+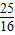 +k2
+k2
=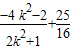 =
=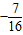 由此可知
由此可知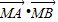 =-
=-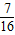 为定值.
为定值.
点评:本题是中档题,考查椭圆方程的求法,直线与椭圆的位置关系,注意余弦定理、面积公式椭圆的定义以及向量数量积的综合应用,考查计算能力,转化思想.
(Ⅱ)利用直线与椭圆方程,通过韦达定理,结合向量的数量积化简得到定值即可.
解答:解:(Ⅰ)设|PF1|=m,|PF2|=n,在三角形PF1F2中,由余弦定理得4=m2+n2-2mncos
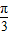 ,由三角形的面积为
,由三角形的面积为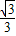
所以
 ,所以mn=
,所以mn= ,所以m+n=2
,所以m+n=2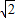 ,所以a=
,所以a=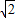 ;又c=1,所以b=1,椭圆C的方程为
;又c=1,所以b=1,椭圆C的方程为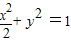 ;
;(Ⅱ)由F2(1,0),直线l的方程为y=k(x-1).由
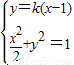 消去y,(2k2+1)x2-4k2x+2(k2-1)=0
消去y,(2k2+1)x2-4k2x+2(k2-1)=0设A(x1,y1),B(x2,y2)则x1+x2=
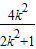 ,x1x2=
,x1x2=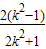
∴
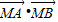 =(x1-
=(x1- ,y1)(x2-
,y1)(x2- ,y2)=(x1-
,y2)=(x1- )(x2-
)(x2- )+y1y2
)+y1y2=(x1-
 )(x2-
)(x2- )+k2(x1-1)(x2-1)
)+k2(x1-1)(x2-1)=(k2+1)
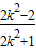 -
-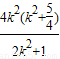 +
+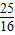 +k2
+k2=
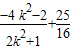 =
=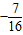 由此可知
由此可知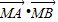 =-
=-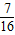 为定值.
为定值.点评:本题是中档题,考查椭圆方程的求法,直线与椭圆的位置关系,注意余弦定理、面积公式椭圆的定义以及向量数量积的综合应用,考查计算能力,转化思想.

练习册系列答案
相关题目
 (a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为
(a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为 +1,且△PF1F2的最大面积为1。
+1,且△PF1F2的最大面积为1。 ,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R,
,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R, 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。