题目内容
(本小题满分12分)已知定义域为R的函数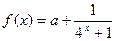 是奇函数.
是奇函数.
(Ⅰ)求 a的值,并指出函数
a的值,并指出函数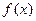 的单调性(不必说明单调性理
的单调性(不必说明单调性理 由);
由);
(Ⅱ)若对任意的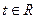 ,不等式
,不等式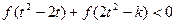 恒成立,求
恒成立,求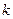 的取值范围.
的取值范围.
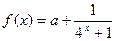 是奇函数.
是奇函数.(Ⅰ)求
 a的值,并指出函数
a的值,并指出函数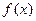 的单调性(不必说明单调性理
的单调性(不必说明单调性理 由);
由);(Ⅱ)若对任意的
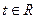 ,不等式
,不等式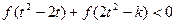 恒成立,求
恒成立,求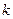 的取值范围.
的取值范围.解:(Ⅰ)函数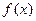 的定义域为R,因为
的定义域为R,因为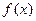 是奇函数,所以
是奇函数,所以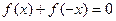 ,
,
即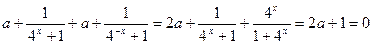 ,故
,故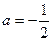 ……4分
……4分
(另解:由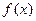 是R上的奇函数,所以
是R上的奇函数,所以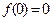 ,故
,故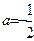 .
.
再由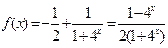 ,
,
通过验证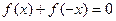 来确定
来确定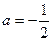 的合理性)
的合理性)  ……………4分
……………4分
由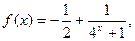 知
知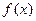 在R上为减函数 ……………6分
在R上为减函数 ……………6分
(Ⅱ)解法一:由(Ⅰ)得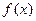 在R上为减函数,
在R上为减函数,
又因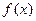 是奇函数,从而不等式
是奇函数,从而不等式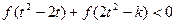 等价于
等价于
 ……………9分
……………9分
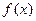 在R上为减函数,由上式得
在R上为减函数,由上式得 :
: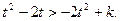
即对一切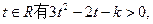
从而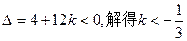
 ……………13分
……………13分
解法二:由(1)知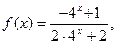 又由题设条件得:
又由题设条件得: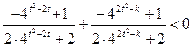
即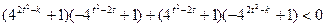
 ……………9分
……………9分
整理得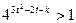
 ,因底数4>1,故
,因底数4>1,故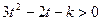
上式对一切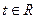 均成立,从而判别式
均成立,从而判别式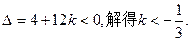 …………13分
…………13分
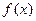 的定义域为R,因为
的定义域为R,因为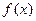 是奇函数,所以
是奇函数,所以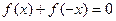 ,
,即
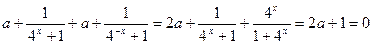 ,故
,故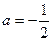 ……4分
……4分(另解:由
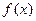 是R上的奇函数,所以
是R上的奇函数,所以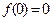 ,故
,故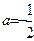 .
.再由
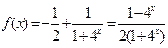 ,
,通过验证
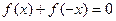 来确定
来确定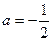 的合理性)
的合理性)  ……………4分
……………4分由
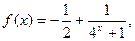 知
知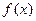 在R上为减函数 ……………6分
在R上为减函数 ……………6分(Ⅱ)解法一:由(Ⅰ)得
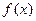 在R上为减函数,
在R上为减函数,又因
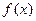 是奇函数,从而不等式
是奇函数,从而不等式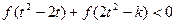 等价于
等价于 ……………9分
……………9分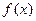 在R上为减函数,由上式得
在R上为减函数,由上式得 :
: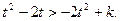
即对一切
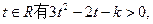
从而
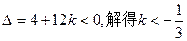
 ……………13分
……………13分解法二:由(1)知
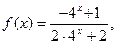 又由题设条件得:
又由题设条件得: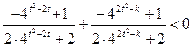
即
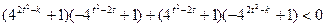
 ……………9分
……………9分整理得
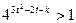
 ,因底数4>1,故
,因底数4>1,故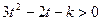
上式对一切
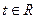 均成立,从而判别式
均成立,从而判别式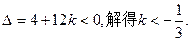 …………13分
…………13分略

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
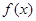 为奇函数,
为奇函数,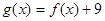 ,
,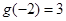 ,求
,求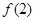
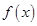 满足
满足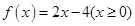 ,则
,则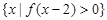 =( )
=( ) 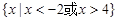
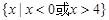
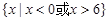
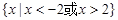
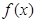 是定义在R上的函数,对任意
是定义在R上的函数,对任意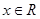 都有
都有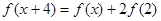 ,若函数
,若函数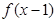 的图象关于直线
的图象关于直线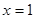 对称,且
对称,且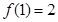 ,则
,则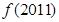 等于( )
等于( )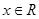 总有
总有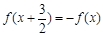 ,则
,则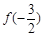 的值为( )
的值为( ) 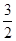
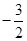
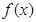 是R上的奇函数,且当
是R上的奇函数,且当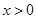 时,
时,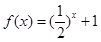 ,则
,则
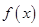 在
在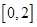 上递减,试比
上递减,试比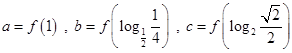 大小
大小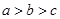
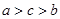
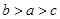
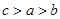
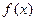 的定义域为
的定义域为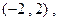 导函数为
导函数为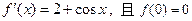 ,则满足
,则满足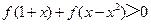
 的实数
的实数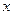 的取值范围为
的取值范围为