题目内容
8.(x2-$\frac{2}{x}$)5的展开式中x4的系数为40(用数字作答).分析 根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为4求得r,再代入系数求出结果.
解答 解:根据所给的二项式写出展开式的通项,Tr+1=${C}_{5}^{r}•(-2)^{r}•{x}^{10-3r}$,
要求x4的项的系数
∴10-3r=4,
∴r=2,
∴x4的项的系数是C52(-2)2=40
故答案为:40
点评 本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则此几何体不可能是( )


| A. | 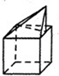 | B. |  | C. |  | D. |  |
16.若不等式(-2)na-3n-1-(-2)n<0对任意正整数n恒成立,则实数a的取值范围是( )
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{1}{2}$,$\frac{4}{3}$) | C. | (1,$\frac{7}{4}$) | D. | ($\frac{1}{2}$,$\frac{7}{4}$) |
3.已知A>0,ω>0,若直线y=b(0<b<A)与函数f(x)=Asin(ωx+φ)的图象的三个相邻交点的横坐标分别是1,3,7,则φ可取( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{11π}{6}$ |
20.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 5 | 7 | 9 | 8 |
| 乙班 | 4 | 8 | 9 | 7 | 7 |
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
18.若某个几何体的三视图如下(单位:cm),则这个几何体的体积是( )


| A. | $\frac{4000}{3}c{m}^{3}$ | B. | $\frac{8000}{3}c{m}^{3}$ | C. | 2000cm3 | D. | 4000cm3 |