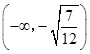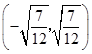题目内容
【题目】已知函数f(x)=e2x(ax2+2x﹣1),a∈R.
(Ⅰ)当a=4时,求证:过点P(1,0)有三条直线与曲线y=f(x)相切;
(Ⅱ)当x≤0时,f(x)+1≥0,求实数a的取值范围.
【答案】解法一:(Ⅰ)证明:当a=4时,f(x)=e2x(4x2+2x﹣1), f'(x)=e2x2(4x2+2x﹣1)+e2x(8x+2)=2e2x(4x2+6x)
设直线与曲线y=f(x)相切,其切点为(x0 , f(x0)),
则曲线y=f(x)在点(x0 , f(x0))处的切线方程为:y﹣f(x0)=f'(x0)(x﹣x0),
因为切线过点P(1,0),所以﹣f(x0)=f'(x0)(1﹣x0),
即 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
设g(x)=8x3﹣14x+1,
∵g(﹣2)=﹣35<0,g(0)=1>0,g(1)=﹣5<0,g(2)=37>0
∴g(x)=0在三个区间(﹣2,0),(0,1),(1,2)上至少各有一个根.
又因为一元三次方程至多有三个根,所以方程8x3﹣14x+1=0恰有三个根,
故过点P(1,0)有三条直线与曲线y=f(x)相切.
(Ⅱ)∵当x≤0时,f(x)+1≥0,即当x≤0时,e2x(ax2+2x﹣1)+1≥0,
∴当x≤0时, ![]() ,
,
设 ![]() ,
,
则 ![]() ,
,
设 ![]() ,则
,则 ![]() .
.
(i)当a≥﹣2时,∵x≤0,∴ ![]() ,从而m'(x)≥0(当且仅当x=0时,等号成立)
,从而m'(x)≥0(当且仅当x=0时,等号成立)
∴ ![]() 在(﹣∞,0]上单调递增,
在(﹣∞,0]上单调递增,
又∵m(0)=0,∴当x≤0时,m(x)≤0,从而当x≤0时,h'(x)≤0,
∴ ![]() 在(﹣∞,0]上单调递减,又∵h(0)=0,
在(﹣∞,0]上单调递减,又∵h(0)=0,
从而当x≤0时,h(x)≥0,即 ![]()
于是当x≤0时,f(x)+1≥0,
(ii)当a<﹣2时,令m'(x)=0,得 ![]() ,∴
,∴ ![]() ,
,
故当 ![]() 时,
时, ![]() ,
,
∴ ![]() 在
在 ![]() 上单调递减,
上单调递减,
又∵m(0)=0,∴当 ![]() 时,m(x)≥0,
时,m(x)≥0,
从而当 ![]() 时,h'(x)≥0,
时,h'(x)≥0,
∴ ![]() 在
在 ![]() 上单调递增,
上单调递增,
又∵h(0)=0,
从而当 ![]() 时,h(x)<0,即
时,h(x)<0,即 ![]()
于是当 ![]() 时,f(x)+1<0,
时,f(x)+1<0,
综合得a的取值范围为[﹣2,+∞).
解法二:(Ⅰ)当a=4时,f(x)=e2x(4x2+2x﹣1),
f'(x)=e2x2(4x2+2x﹣1)+e2x(8x+2)=2e2x(4x2+6x),
设直线与曲线y=f(x)相切,其切点为(x0 , f(x0)),
则曲线y=f(x)在点(x0 , f(x0))处的切线方程为y﹣f(x0)=f'(x0)(x﹣x0),
因为切线过点P(1,0),所以﹣f(x0)=f'(x0)(1﹣x0),)
即 ![]() ,
,
∵ ![]() ,∴
,∴ ![]()
设g(x)=8x3﹣14x+1,则g'(x)=24x2﹣14,令g'(x)=0得 ![]() ,
,
当x变化时,g(x),g'(x)变化情况如下表:
x |
|
|
|
|
|
g'(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴8x3﹣14x+1=0恰有三个根,
故过点P(1,0)有三条直线与曲线y=f(x)相切.
(Ⅱ)同解法一
【解析】(Ⅰ)方法一、求出f(x)的解析式和导数,设直线与曲线y=f(x)相切,其切点为(x0 , f(x0)),求出切线的方程,代入P的坐标,整理成三次方程,运用两点存在定理,考虑方程的根的情况即可得证; 方法二、求出f(x)的解析式和导数,设直线与曲线y=f(x)相切,其切点为(x0 , f(x0)),求出切线的方程,代入P的坐标,整理成三次方程,构造三次函数,求出导数和单调区间及极值,即可得证;(Ⅱ)由题意可得当x≤0时,e2x(ax2+2x﹣1)+1≥0,构造 ![]() ,设
,设 ![]() ,求出导数,讨论a的范围,运用单调性即可得到a的范围.
,求出导数,讨论a的范围,运用单调性即可得到a的范围.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.