题目内容
由函数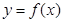 确定数列
确定数列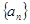 ,
,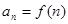 .若函数
.若函数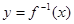 能确定数列
能确定数列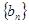 ,
,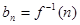 ,则称数列
,则称数列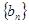 是数列
是数列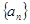 的“反数列”.
的“反数列”.
(1)若函数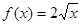 确定数列
确定数列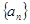 的反数列为
的反数列为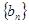 ,求
,求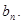 ;
;
(2)对(1)中的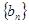 ,不等式
,不等式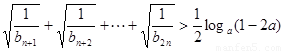 对任意的正整数
对任意的正整数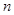 恒成立,求实数
恒成立,求实数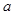 的取值范围;
的取值范围;
(3)设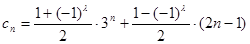 (
(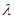 为正整数),若数列
为正整数),若数列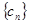 的反数列为
的反数列为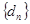 ,
,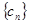 与
与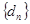 的公共项组成的数列为
的公共项组成的数列为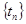 (公共项
(公共项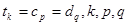 为正整数),求数列
为正整数),求数列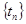 的前
的前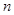 项和
项和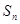 .
.
【答案】
(1)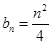 ;(2)
;(2)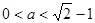 ;(3)
;(3)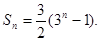
【解析】
试题分析:(1)本题实质是求函数 的反函数
的反函数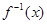 ;(2)不等式恒成立,因此
;(2)不等式恒成立,因此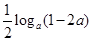 小于不等式左边的最小值,所以我们一般想办法求左边
小于不等式左边的最小值,所以我们一般想办法求左边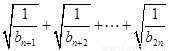 这个和,然而由(1)知
这个和,然而由(1)知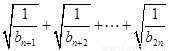
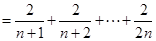 ,这个和求不出,那么我们只能从另一角度去思考,看
,这个和求不出,那么我们只能从另一角度去思考,看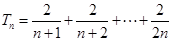 的单调性,这里只要作差
的单调性,这里只要作差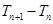 就可得出
就可得出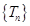 是递增数列,所以
是递增数列,所以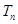 的最小值是
的最小值是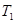 ,问题解决;(3)看起来
,问题解决;(3)看起来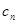 很复杂,实质上由于
很复杂,实质上由于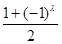 和
和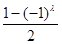 取值只能是0和1,因此我们按
取值只能是0和1,因此我们按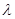 的奇偶性分类讨论,问题就简化了,例如当
的奇偶性分类讨论,问题就简化了,例如当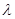 为奇数时,
为奇数时,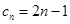 ,则
,则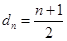 ,就可求出
,就可求出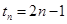 ,从而求出
,从而求出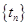 的前
的前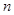 项和了.
项和了.
试题解析:(1)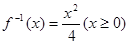 ,则
,则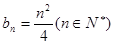 ;4分
;4分
(2)不等式化为: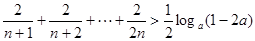 ,5分
,5分
设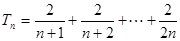 ,因为
,因为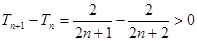 ,
,
所以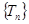 单调递增,
7分
单调递增,
7分
则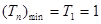 .因此
.因此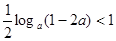 ,即
,即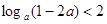 .因为
.因为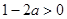 ,
,
所以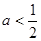 ,
,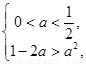 得
得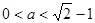 .
10分
.
10分
(3)当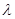 为奇数时,
为奇数时,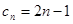 ,
,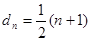 .
11分
.
11分
由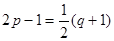 ,则
,则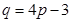 ,
,
即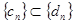 ,因此
,因此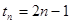 ,
13分
,
13分
所以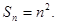 14分
14分
当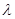 为偶数时,
为偶数时,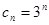 ,
,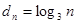 .
15分
.
15分
由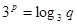 得
得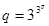 ,即
,即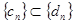 ,因此
,因此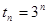 , 17分
, 17分
所以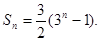 18分
18分
考点:(1)反函数;(2)数列的单调性;(3)分类讨论,等差数列与等比数列的前 项和.
项和.

练习册系列答案
相关题目
 ,写出
,写出