题目内容
(理)已知平面内动点P(x,y)到定点F(| 5 |
| 4 | ||
|
| ||
| 2 |
( I)求动点P的轨迹C及其方程;
( II)求过点Q(2,1)且与曲线C有且仅有一个公共点的直线方程.
分析:( I)利用双曲线定义,可知到定点F(
,0)与定直线l:x=
的距离之比是常数
的点的轨迹为双曲线,在利用求双曲线方程的方法去解即可.
( II)与双曲线C有且仅有一个公共点的直线有两种,一种是与双曲线相切,一种是平行渐近线,分两种情况考虑即可.
| 5 |
| 4 | ||
|
| ||
| 2 |
( II)与双曲线C有且仅有一个公共点的直线有两种,一种是与双曲线相切,一种是平行渐近线,分两种情况考虑即可.
解答:解:( I)∵
>1,
∴轨迹C为以F为右焦点,l为右准线的双曲线.
设双曲线C方程为
-
=1(a>0,b>0),则
,
∴a2=4.
∴b2=c2-a2=5-4=1.
∴双曲线方程为
-y2=1.
(Ⅱ)(1)若所求直线斜率不存在时,直线x=2满足题意.
(2)若所求直线斜率存在时,设所求直线方程为y-1=k(x-2),
代入曲线方程
-y2=1,得:
-(kx-2k+1)2=1,
化简得:(1-4k2)x2+8k(2k-1)x-4(2k-1)2-4=0,
①当(1-4k2)=0时,即k=±
时,
∵(2,1)在渐近线y=
x上,∴k=
时不适合,舍去.k=-
时,直线平行于渐近线y=-
x,满足题意,
故所求直线方程为y=-
(x-2)+1,即y=-
x+2.
②当(1-4k2)≠0时,由△=64k2(2k-1)2-16(4k2-1)(4k2-4k+2)=0,
得k=
(舍去),综上所述,所求直线方程为x=2,y=-
x+2.
| ||
| 2 |
∴轨迹C为以F为右焦点,l为右准线的双曲线.
设双曲线C方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
∴a2=4.
∴b2=c2-a2=5-4=1.
∴双曲线方程为
| x2 |
| 4 |
(Ⅱ)(1)若所求直线斜率不存在时,直线x=2满足题意.
(2)若所求直线斜率存在时,设所求直线方程为y-1=k(x-2),
代入曲线方程
| x2 |
| 4 |
| x2 |
| 4 |
化简得:(1-4k2)x2+8k(2k-1)x-4(2k-1)2-4=0,
①当(1-4k2)=0时,即k=±
| 1 |
| 2 |
∵(2,1)在渐近线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故所求直线方程为y=-
| 1 |
| 2 |
| 1 |
| 2 |
②当(1-4k2)≠0时,由△=64k2(2k-1)2-16(4k2-1)(4k2-4k+2)=0,
得k=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了双曲线方程的求法,以及直线与双曲线位置关系的判断,计算量较大,应认真计算.

练习册系列答案
相关题目
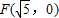 与定直线l:
与定直线l: 的距离之比是常数
的距离之比是常数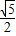 .
.