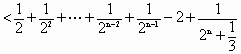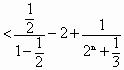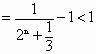题目内容
| |||||||||||||||||||
答案:
解析:
解析:
(1) |
解: ∴xn+1xn=xn+2……………………………………………………(4分) |
(2) |
解: ∴ 又 ∴ ∴ ∴ |
(3) |
证明: ∴ 当n为奇数时,
①当n为偶数时, ②当n为奇数时,
综上, |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
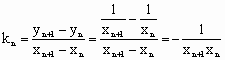 …………………………(2分)
…………………………(2分)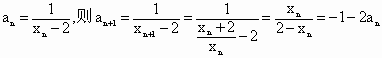 …………………………(7分)
…………………………(7分) …………………………(10分)
…………………………(10分)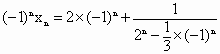

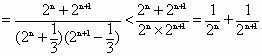 …………………………(12分)
…………………………(12分)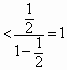 …………………………(13分)
…………………………(13分)