题目内容
如图中阴影部分表示的平面区域可用二元一次不等式组表示成（ ）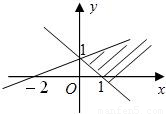
A．
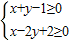
B．
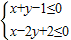
C．
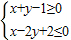
D．
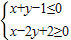
【答案】分析：由图解出两个边界直线对应的方程，由二元一次不等式与区域的对应关系从选项中选出正确选项．
解答：解：由图知，一边界过（0，1），（1，0）两点，故其直线方程为x+y-1=0
另一边界直线过（0，1），（-2，0）两点，故其直线方程为x-2y+2=0
由不等式与区域的对应关系知区域应满足x+y-1≥0与x-2y+2≥0
故区域对应的不等式组为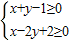
故选A．
点评：考查用两点法求直线方程与二元一次方程与区域的对应关系，是基本概念应用的题型．
解答：解：由图知，一边界过（0，1），（1，0）两点，故其直线方程为x+y-1=0
另一边界直线过（0，1），（-2，0）两点，故其直线方程为x-2y+2=0
由不等式与区域的对应关系知区域应满足x+y-1≥0与x-2y+2≥0
故区域对应的不等式组为
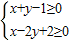
故选A．
点评：考查用两点法求直线方程与二元一次方程与区域的对应关系，是基本概念应用的题型．
练习册系列答案
相关题目
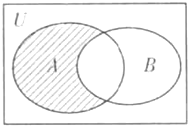（2013•韶关二模）设全集U=R，集合A={x|x（x+3）＜0}，B={x|x＜-1}，则如图中阴影部分表示的集合为
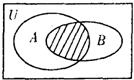设全集U=R，A={x|x（-x-3）＞0}，B={x|y=ln（-x-1）}，则如图中阴影部分表示的集合为（ ）
若全集U=R，集合M={x|-x2-x+2＜0}，N={x|x-1＜0}，则如图中阴影部分表示的集合是（ ）
已知全集U=R，集合A={x|x＜3，或x＞4}，B={x|x＜2}，则如图中阴影部分表示的集合为（ ）