题目内容
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,
第3小题满分7分.
对定义在区间 上的函数
上的函数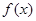 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意的
,使得对任意的 都有
都有 ,且对任意的
,且对任意的 都有
都有 恒成立,则称函数
恒成立,则称函数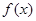 为区间
为区间 上的“U型”函数。
上的“U型”函数。
(1)求证:函数 是
是 上的“U型”函数;
上的“U型”函数;
(2)设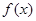 是(1)中的“U型”函数,若不等式
是(1)中的“U型”函数,若不等式 对一切的
对一切的 恒成立,
恒成立,
求实数 的取值范围;
的取值范围;
(3)若函数 是区间
是区间 上的“U型”函数,求实数
上的“U型”函数,求实数 和
和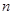 的值.
的值.
【答案】
解:(1)当 时,
时,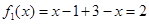
当 时,
时,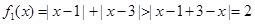
故存在闭区间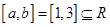 和常数C=2符合条件,…………………………4分
和常数C=2符合条件,…………………………4分
所以函数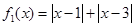 是
是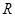 上的“U型”函数…………………………5分
上的“U型”函数…………………………5分
(2)因为不等式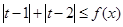 对一切的
对一切的 恒成立,
恒成立,
所以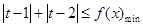 …………………………7分
…………………………7分
由(1)可知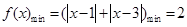 …………………8分
…………………8分
所以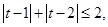 …………………………9分
…………………………9分
解得: …………………………11分
…………………………11分
(3)由“U型”函数定义知,存在闭区间 和常数
和常数 ,使得对任意的
,使得对任意的 ,
,
都有
即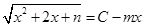
所以 对任意的
对任意的 成立……………13分
成立……………13分
所以 …………………………14分
…………………………14分
 ①当
①当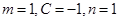 时,
时,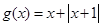
当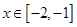 时,
时,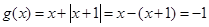
当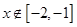 ,即
,即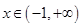 时,
时,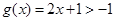
由题意知, 符合条件…………………………16分
符合条件…………………………16分
②当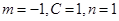 时,
时,
当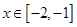 时,
时,
当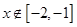 ,即
,即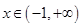 时,
时,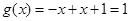
由题意知, 不符合条件
不符合条件
综上所述, …………………………18分
…………………………18分
【解析】略

练习册系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处