题目内容
已知f(x)=logmx(m为常数,m>0且m≠1)
设f(a1),f(a2),…,f(an)(n∈N+)是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
(2)若bn=an•f(an),且数列{bn}的前n项和Sn,当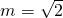 时,求Sn.
时,求Sn.
解:(1)由题意f(an)=4+2(n-1)=2n+2,
即logman=2n+2
∴an=m2n+2
∴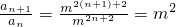
∵m>0且m≠1,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列
(2)由题意bn=anf(an)=m2n+2logmm2n+2=(2n+2)•m2n+2,
当
∴Sn=2•23+3•24+4•25+…+(n+1)•2n+2①
①式两端同乘以2,得2Sn=2•24+3•25+4•26+…+n•2n+2+(n+1)•2n+3②
②-①并整理,得Sn=-2•23-24-25-26-…-2n+2+(n+1)•2n+3
=-23-[23+24+25+…+2n+2]+(n+1)•2n+3
=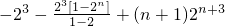
=-23+23(1-2n)+(n+1)•2n+3=2n+3•n
分析:(1)利用等差数列的通项公式求出f(an),利用对数的定义求出an,求出相邻两项的比,利用等比数列的定义得证.
(2)求出bn,将m的值代入,利用错位相减法求出数列的前n项和Sn.
点评:要证明一个数列是等差数列(等比数列)一般利用两个特殊数列的定义;求数列的前n项和,首先判断数列的通项的特点,再选择合适的方法.
即logman=2n+2
∴an=m2n+2
∴
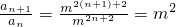
∵m>0且m≠1,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列
(2)由题意bn=anf(an)=m2n+2logmm2n+2=(2n+2)•m2n+2,
当

∴Sn=2•23+3•24+4•25+…+(n+1)•2n+2①
①式两端同乘以2,得2Sn=2•24+3•25+4•26+…+n•2n+2+(n+1)•2n+3②
②-①并整理,得Sn=-2•23-24-25-26-…-2n+2+(n+1)•2n+3
=-23-[23+24+25+…+2n+2]+(n+1)•2n+3
=
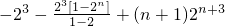
=-23+23(1-2n)+(n+1)•2n+3=2n+3•n
分析:(1)利用等差数列的通项公式求出f(an),利用对数的定义求出an,求出相邻两项的比,利用等比数列的定义得证.
(2)求出bn,将m的值代入,利用错位相减法求出数列的前n项和Sn.
点评:要证明一个数列是等差数列(等比数列)一般利用两个特殊数列的定义;求数列的前n项和,首先判断数列的通项的特点,再选择合适的方法.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |