题目内容
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集为空集,求实数
的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2)![]()
【解析】试题分析:(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集(2)先根据绝对值定义将函数化为分段函数,求对应函数值域,即得f(x)﹣4的取值范围,根据倒数性质可得![]() 取值范围,最后根据方程解集为空集,确定实数
取值范围,最后根据方程解集为空集,确定实数![]() 的取值范围
的取值范围
试题解析:解:(1)解不等式|x﹣2|+|2x+1|>5,
x≥2时,x﹣2+2x+1>5,解得:x>2;
﹣![]() <x<2时,2﹣x+2x+1>5,无解,
<x<2时,2﹣x+2x+1>5,无解,
x≤﹣![]() 时,2﹣x﹣2x﹣1>5,解得:x<﹣
时,2﹣x﹣2x﹣1>5,解得:x<﹣![]() ,
,
故不等式的解集是(﹣∞,﹣![]() )∪(2,+∞);
)∪(2,+∞);
(2)f(x)=|x﹣2|+|2x+1|=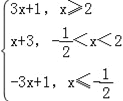 ,
,
故f(x)的最小值是![]() ,所以函数f(x)的值域为[
,所以函数f(x)的值域为[![]() ,+∞),
,+∞),
从而f(x)﹣4的取值范围是[﹣![]() ,+∞),
,+∞),
进而![]() 的取值范围是(﹣∞,﹣
的取值范围是(﹣∞,﹣![]() ]∪(0,+∞).
]∪(0,+∞).
根据已知关于x的方程![]() =a的解集为空集,所以实数a的取值范围是(﹣
=a的解集为空集,所以实数a的取值范围是(﹣![]() ,0].
,0].

练习册系列答案
相关题目