题目内容
已知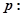 存在
存在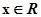 ,使
,使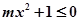 ;
;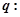 对任意
对任意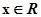 ,恒有
,恒有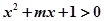 。
。
若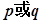 为假命题,则实数m的取值范围为
为假命题,则实数m的取值范围为
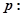 存在
存在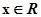 ,使
,使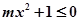 ;
;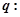 对任意
对任意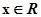 ,恒有
,恒有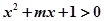 。
。若
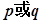 为假命题,则实数m的取值范围为
为假命题,则实数m的取值范围为 A.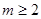 | B.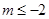 | C. | D.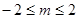 |
A
分析:先求出p,q是真命题的x的范围,由于p或q为假命题,得到p,q应该全假,即p,q的否定为真,列出方程组,求出m的范围.
解答:解:若p真则m<0;
若q真,即x2+mx+1>0恒成立,
所以△=m2-4<0,
解得-2<m<2.
因为p或q为假命题,所以p,q全假.
所以有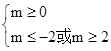 ,
,
所以m≥2.
故选A
解答:解:若p真则m<0;
若q真,即x2+mx+1>0恒成立,
所以△=m2-4<0,
解得-2<m<2.
因为p或q为假命题,所以p,q全假.
所以有
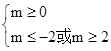 ,
,所以m≥2.
故选A

练习册系列答案
相关题目
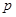 :
: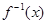 是
是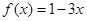 的反函数,且
的反函数,且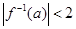 ;命题
;命题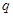 :集合
:集合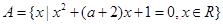 ,
,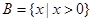 ,且
,且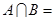 Ф.
Ф.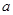 的取值范围。
的取值范围。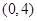 到实数集
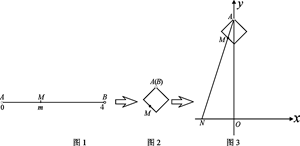
到实数集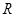 的映射过程:区间
的映射过程:区间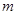 对应数轴上的点
对应数轴上的点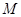 (如图1),将线段
(如图1),将线段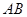 围成一个正方形,使两端点
围成一个正方形,使两端点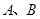 恰好重合(如图2),
恰好重合(如图2),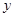 轴上,点
轴上,点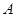 的坐标为
的坐标为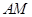 与
与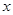 轴交于点
轴交于点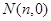 ,则
,则 ,记作
,记作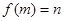 .
.
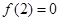 ; ②
; ②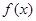 的图象关于点
的图象关于点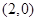 对称;
对称;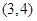 上为常数函数; ④
上为常数函数; ④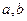 都是偶数,则
都是偶数,则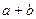 是偶数”的否命题是
是偶数”的否命题是 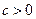 ,设
,设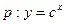 在R上单调递减,
在R上单调递减,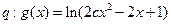 的定义域为R,如果“
的定义域为R,如果“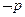 或
或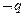 ”为真命题,“
”为真命题,“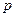 或
或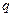 ”也为真命题,则实数
”也为真命题,则实数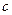 的取值范围是______▲___.
的取值范围是______▲___.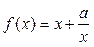 在区间[1,2]上单调递增;
在区间[1,2]上单调递增; 命题Q:不等式
命题Q:不等式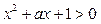 对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是 ( )
对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是 ( )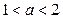 B
B 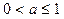

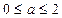 D
D 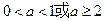
 ①“若对所有满足
①“若对所有满足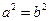 的
的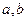 ,都有
,都有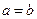 ”的否命题;
”的否命题;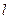 的方向向量为
的方向向量为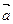 =(1,
=(1,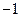 ,2),平面
,2),平面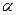 的法向量为
的法向量为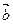 =(-2,0,1),
=(-2,0,1),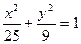 与曲线
与曲线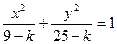 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点;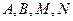 是空间四点,若
是空间四点,若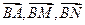 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么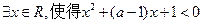 ”是真命题,则实数
”是真命题,则实数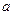 的取值范围
的取值范围