题目内容
20．
已知函数f（x）=x|x-m|，x∈R，且f（4）=0．（1）求实数m的值；
（2）作出函数f（x）的图象并直接写出f（x）单调减区间．
分析 （1）由f（4）=0，代入解方程可得m=4；
（2）将f（x）写成分段函数的形式，画出图象，再由图象观察可得单调减区间．
解答 
解：（1）依题意f（4）=4|4-m|=0，
所以m=4；
（2）函数f（x）=x|x-4|=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥4}\\{4x-{x}^{2}，x＜4}\end{array}\right.$，
图象如图所示：
由图象可得，f（x）的单调减区间为：（2，4）．
点评 本题考查函数的解析式的求法和图象的画法，以及单调区间的求法，考查数形结合的思想方法，属于基础题．
练习册系列答案
相关题目
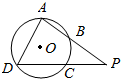如图，四边形ABCD是⊙O的内接四边形，延长AB和DC相交于点P，若$\frac{PB}{PA}$=$\frac{1}{2}$，$\frac{PC}{PD}$=$\frac{1}{3}$，则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$．
11．若曲线x2-4x+y2-2y+4=0（y≥1）与直线y=k（x+1）有2个公共点，则k的取值范围是（ ）
| A． | （0，$\frac{1}{2}$] | B． | （$\frac{1}{4}$，$\frac{3}{4}$] | C． | [$\frac{1}{2}$，$\frac{3}{4}$） | D． | [$\frac{1}{4}$，1） |