题目内容
已知正项等比数列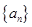 满足:
满足: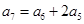 ,若存在两项
,若存在两项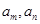 使得
使得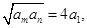 则
则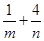 的最小值为( ).
的最小值为( ).
A.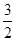 | B.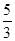 | C.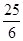 | D.不存在 |
A
解析试题分析:因为,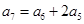 ,所以,a5q2=a5q+2a5,q2-q-2=0,解得,q=2。
,所以,a5q2=a5q+2a5,q2-q-2=0,解得,q=2。
又因为,存在两项am,an使得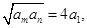 所以aman=16a12,
所以aman=16a12,
所以,qm+n-2=16, m+n=6。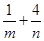 =
=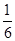 (
(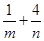 )(m+n)
)(m+n)
=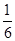 (5+
(5+  )≥
)≥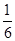 (5+4)=
(5+4)=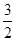 ,故选A。
,故选A。
考点:本题主要考查等比数列的通项公式,均值定理的应用。
点评:小综合题,通过利用等比数列的知识,得到m+n为定值,从而具备了应用均值定理的两个条件,再通过构造,其第三个条件“三相等”,也具备了。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
设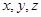 是不相等的三个数,则使
是不相等的三个数,则使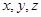 成等差数列, 且
成等差数列, 且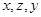 成等比数列的条件是( )
成等比数列的条件是( )
A.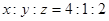 | B.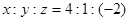 |
C.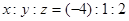 | D.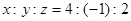 |
 和
和 的等比中项是 ( )
的等比中项是 ( )
| A. 1 | B.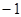 | C.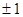 | D. 2 |
设等比数列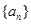 的公比
的公比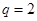 ,前n项和为
,前n项和为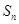 ,则
,则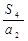 的值是( )
的值是( )
A.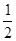 | B.4 | C.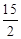 | D.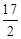 |
数列 前
前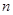 项和为
项和为 ,已知
,已知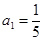 ,且对任意正整数
,且对任意正整数 ,都有
,都有 ,若
,若 恒成立,则实数
恒成立,则实数 的最小值为( )
的最小值为( )
A. | B.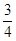 | C.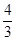 | D.4 |
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
已知等比数列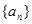 中,各项都是正数,且
中,各项都是正数,且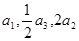 成等差数列,则
成等差数列,则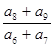 =( )
=( )
A.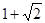 | B.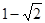 | C.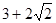 | D.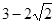 |
在等比数列{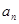 }中,若
}中,若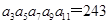 ,则
,则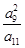 的值为
的值为
| A.9 | B.1 | C.2 | D.3 |