题目内容
已知不等式 对任意正实数x,y恒成立,则正实数a的最小值为( )
对任意正实数x,y恒成立,则正实数a的最小值为( )A.2
B.4
C.8
D.16
【答案】分析:要使不等式恒成立,即左边的最小值大于等于8-a,将左边展开利用基本不等式求出左边的最小值,列出不等式解得.
解答:解:因为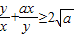 ,当且仅当
,当且仅当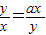 ,时等号成立,
,时等号成立,
又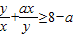 .正实数a,对任意正实数x,y恒成立,
.正实数a,对任意正实数x,y恒成立,
所以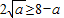 .
.
解得16≥a≥4.
故a的最小值为4.
故选B.
点评:本题考查利用基本不等式求函数最值要注意满足的条件:一正、二定、三相等.
解答:解:因为
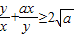 ,当且仅当
,当且仅当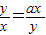 ,时等号成立,
,时等号成立,又
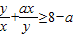 .正实数a,对任意正实数x,y恒成立,
.正实数a,对任意正实数x,y恒成立,所以
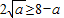 .
.解得16≥a≥4.
故a的最小值为4.
故选B.
点评:本题考查利用基本不等式求函数最值要注意满足的条件:一正、二定、三相等.

练习册系列答案
相关题目
 既无最小值也无最大值;
既无最小值也无最大值; 上随机取一个数
上随机取一个数 ,使得
,使得 成立的概率为
成立的概率为 ;
; 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为16;
的最小值为16; ,若方程
,若方程 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数 的取值范围是
的取值范围是 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______. 为极点,
为极点, 轴的正半轴为极轴。已知点
轴的正半轴为极轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,圆
,圆 以
以 为半径。
为半径。 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围. ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=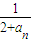 (n∈N*).已知不等式|f(x)≤2x2+4x-30|对任意实数x均成立.
(n∈N*).已知不等式|f(x)≤2x2+4x-30|对任意实数x均成立. )n]≤Sn<2.
)n]≤Sn<2.