题目内容
有以下四个命题:
(1)函数f(x)=x2ex既无最小值也无最大值;
(2)在区间[-3,3]上随机取一个数x,使得|x-1|+|x+2|≤5成立的概率为
;
(3)若不等式(m+n)(
+
)≥25对任意正实数m,n恒成立,则正实数a的最小值为16;
(4)已知函数f(x)=
,若方程f(x)=k(x+2)-2恰有三个不同的实根,则实数k的取值范围是k∈(0,2);
以上正确的序号是: .
(1)函数f(x)=x2ex既无最小值也无最大值;
(2)在区间[-3,3]上随机取一个数x,使得|x-1|+|x+2|≤5成立的概率为
| 5 |
| 6 |
(3)若不等式(m+n)(
| a |
| m |
| 1 |
| n |
(4)已知函数f(x)=
|
以上正确的序号是:
分析:(1)利用导数求函数f(x)=x2ex最值情况;
(2)利用几何概型的概率公式进行判断;
(3)利用基本不等式成立的条件进行判断;
(4)利用数形结合,判断方程根的取值情况.
(2)利用几何概型的概率公式进行判断;
(3)利用基本不等式成立的条件进行判断;
(4)利用数形结合,判断方程根的取值情况.
解答:解:(1)f′(x)=xex(2+x).令f′(x)=0,解得x=0或-2.
由f′(x)>0,解得x>0或x<-2,
∴函数f(x)在(-∞,-2)和(0,+∞)单调递增;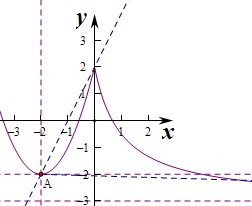
由f′(x)<0,解得-2<x<0,
∴函数f(x)在(-2,0上单调递减.
∴函数f(x)在x=0取得极小值,同时也是最小值f(0)=0;在x=-2取得极大值,f(-2)=
.∴(1)错误.
(2)|x-1|+|x+2|=
,
则当x<-2,由|x-1|+|x+2|≤5得-2x-1≤5,即2x≥-6,解得-3≤x<-2.
当-2≤x≤1,由|x-1|+|x+2|≤5得3≤5,恒成立,此时-2≤x≤1.
当x>1,由|x-1|+|x+2|≤5得2x+1≤5,即x≤2,解得1<x≤2,
综上:不等式|x-1|+|x+2|≤5的解为-3≤x≤2.
∴在区间[-3,3]上随机取一个数x,使得|x-1|+|x+2|≤5成立的概率为
=
,∴(2)正确.
(3)由(m+n)(
+
)=a+1+
+
≥a+1+2
=a+2
+1=(
+1)2,
要使不等式(m+n)(
+
)≥25对任意正实数m,n恒成立,
则(
+1)2≥25,即
+1≥5,即
≥4,
∴a≥16,则正实数a的最小值为16,∴(3)正确.
(4)作出函数f(x)的图象如图:函数y=k(x+2)-2表示过点A(-2,-2)的直线,当直线的斜率k=0时,此时方程f(x)=k(x+2)-2有两个不同的根,
当直线经过点(0,2),即k=2时,方程f(x)=k(x+2)-2有两个不同的根,即当k∈(0,2)时,方程f(x)=k(x+2)-2恰有三个不同的实根,
由图象可知当k<0时,方程f(x)=k(x+2)-2也存在三个不同的实根,∴(4)错误.
故答案为:(2)(3).
由f′(x)>0,解得x>0或x<-2,
∴函数f(x)在(-∞,-2)和(0,+∞)单调递增;

由f′(x)<0,解得-2<x<0,
∴函数f(x)在(-2,0上单调递减.
∴函数f(x)在x=0取得极小值,同时也是最小值f(0)=0;在x=-2取得极大值,f(-2)=
| 4 |
| e2 |
(2)|x-1|+|x+2|=
|
则当x<-2,由|x-1|+|x+2|≤5得-2x-1≤5,即2x≥-6,解得-3≤x<-2.
当-2≤x≤1,由|x-1|+|x+2|≤5得3≤5,恒成立,此时-2≤x≤1.
当x>1,由|x-1|+|x+2|≤5得2x+1≤5,即x≤2,解得1<x≤2,
综上:不等式|x-1|+|x+2|≤5的解为-3≤x≤2.
∴在区间[-3,3]上随机取一个数x,使得|x-1|+|x+2|≤5成立的概率为
| 2-(-3) |
| 3-(-3) |
| 5 |
| 6 |
(3)由(m+n)(
| a |
| m |
| 1 |
| n |
| an |
| m |
| m |
| n |
|
| a |
| a |
要使不等式(m+n)(
| a |
| m |
| 1 |
| n |
则(
| a |
| a |
| a |
∴a≥16,则正实数a的最小值为16,∴(3)正确.
(4)作出函数f(x)的图象如图:函数y=k(x+2)-2表示过点A(-2,-2)的直线,当直线的斜率k=0时,此时方程f(x)=k(x+2)-2有两个不同的根,
当直线经过点(0,2),即k=2时,方程f(x)=k(x+2)-2有两个不同的根,即当k∈(0,2)时,方程f(x)=k(x+2)-2恰有三个不同的实根,
由图象可知当k<0时,方程f(x)=k(x+2)-2也存在三个不同的实根,∴(4)错误.
故答案为:(2)(3).
点评:本题主要考查函数的性质的综合应用,涉及的知识点较大,综合性较强,难度较大.

练习册系列答案
相关题目
 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题: