题目内容
(2012•钟祥市模拟)在△ABC中,E,F分别是AC,AB的中点,且3AB=2AC,若
<t恒成立,则t的最小值为( )
| BE |
| CF |
分析:根据题意画出相应的图形,要求t的最小值,即要求BE与CF比值的最大值,方法为:由AB与AC的关系,用AB表示出AC,由E、F分别为AC、AB的中点,在三角形ABE中,由AB,AE及∠A,利用余弦定理表示出BE2,在三角形ACF中,由AF,AC及∠A,利用余弦定理表示出CF2,并表示出BE与CF的平方比,开方并分离出常数,由A为三角形的内角,得到A的范围,观察表示出的比值发现当cosA的值最小时,比值最大,故当A趋于π时,cosA趋于-1,此时比值最大,求出此时的最大值,即可得到t的取值范围.
解答:解:根据题意画出图形,如图所示:
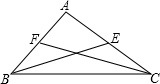
∵3AB=2AC,
∴AC=
AB,
又E、F分别为AC、AB的中点,∴AE=
AC,AF=
AB,
∴在△ABE中,由余弦定理得:BE2=AB2+AE2-2AB•AE•cosA
=AB2+(
AB)2-2AB•
AB•cosA=
AB2-
AB2cosA,
在△ACF中,由余弦定理得:CF2=AF2+AC2-2AF•AC•cosA
=(
AB)2+(
AB)2-2•
AB•
AB•cosA=
AB2-
AB2cosA,
∴
=
=
,
∴
=
=
,
∵当cosA取最小值时,
比值最大,
∴当A→π时,cosA→-1,此时
达到最大值,最大值为
=
,
则
<t恒成立,t的最小值为
.
故选B

∵3AB=2AC,
∴AC=
| 3 |
| 2 |
又E、F分别为AC、AB的中点,∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴在△ABE中,由余弦定理得:BE2=AB2+AE2-2AB•AE•cosA
=AB2+(
| 3 |
| 4 |
| 3 |
| 4 |
| 25 |
| 16 |
| 3 |
| 2 |
在△ACF中,由余弦定理得:CF2=AF2+AC2-2AF•AC•cosA
=(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∴
| BE2 |
| CF2 |
| ||||
|
| ||||
|
∴
| BE |
| CF |
|
1-
|
∵当cosA取最小值时,
| BE |
| CF |
∴当A→π时,cosA→-1,此时
| BE |
| CF |
1-
|
| 7 |
| 8 |
则
| BE |
| CF |
| 7 |
| 8 |
故选B
点评:此题考查了余弦定理,余弦函数的定义域与值域,以及不等式恒成立时满足的条件,余弦定理建立了三角形的边角关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目