Question

（2012•钟祥市模拟）设x，y满足

3x-y-6≤0 x-y+2≥0 x+y≥3

，若目标函数z=ax+y（a＞0）最大值为14，则a为（　　）

• A．

  53

  9

• B．23
• C．2
• D．1

Answer 1

分析：由线性约束条件画出可行域，然后结合目标函数的最大值．求出a的值．

解答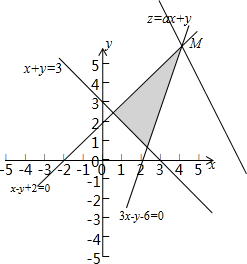：解：画出约束条件

3x-y-6≤0 x-y+2≥0 x+y≥3

的可行域，如图：目标函数z=ax+y（a＞0）最大值为14，即目标函数z=ax+y（a＞0）在

3x-y-6≤0 x-y+2≥0

的交点M（4，6）处，目标函数z最大值为14，
所以4a+6=14，所以a=2．
故选C．

点评：本题直接考查线性规划问题，是一道较为简单的送分题．近年来高考线性规划问题高考数学考试的热点，正确作出可行域是解题的关键．