题目内容
【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上为单调增函数。
在定义域上为单调增函数。
①求![]() 的最大整数值;
的最大整数值;
②证明:![]()
【答案】(1) ![]() .
.
(2) ①2;②证明见解析.
【解析】分析:(1)当![]() 时,化简函数的解析式,求出函数的导数,求出斜率,然后利用点斜式求函数
时,化简函数的解析式,求出函数的导数,求出斜率,然后利用点斜式求函数![]() 的图象在
的图象在![]() 处的切线方程;(2)①函数
处的切线方程;(2)①函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立.先证明
恒成立.先证明![]() ,设
,设![]() ,则
,则![]() ,推出
,推出
当![]() 时,
时,![]() 恒成立,当
恒成立,当![]() 时,
时,![]() ,即
,即![]() 不恒成立,可得
不恒成立,可得![]() 的最大整数值为
的最大整数值为![]() ;②由①知,
;②由①知,![]() ,令
,令![]() ,由此可知,当
,由此可知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .....;当
.....;当![]() 时,
时,![]() ,即可得出结论.
,即可得出结论.
详解:(1)当![]() 时,
时,![]()
∴![]()
又![]() ,
,
所以![]()
所求切线方程为![]() ,即
,即![]()
(2)由题意知,![]()
若函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立,
恒成立,
①先证明![]() ,设
,设![]() ,则
,则![]()
则函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
所以![]() ,即
,即![]()
同理可证![]() ,
,
所以![]() ,
,
所以![]()
当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,即
,即![]() 不恒成立
不恒成立
综上所述,![]() 的最大整数值为
的最大整数值为![]()
②由①知,![]() ,令
,令![]()
所以![]() ,
,
所以![]()
由此可知,当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() .....,
.....,
当![]() 时,
时,![]()
累加得![]()
又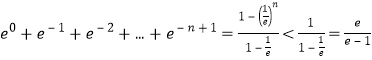
所以![]()
即![]()

练习册系列答案
相关题目
