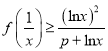Question

【题目】如图一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为,设∠AOE=,探照灯O照射在长方形ABCD内部区域的面积为S.

(1)当0≤时,写出S关于的函数表达式;

(2)若探照灯每9分钟旋转“一个来回”(OE自OA转到OC,再回到OA,称“一个来回”,忽略OE在OA及OC反向旋转时所用时间),且转动的角速度大小一定,设AB边上有一点G,且∠AOG,求点G在“一个来回”中,被照到的时间.

Answer 1

【答案】(1),S(2)2分钟

【解析】

(1) 根据AD=2，AB=1，0≤，确定点E，F的位置，分0≤，，两种情况，利用三角形面积公式求解.

(2)先得到“一个来回”中，OE共转了2，其中点G被照到时，共转了2，再利用角度关系求解.

如图所示：

(1)过O作OH⊥BC，H为垂足.

①当0≤时，E在边AB上，F在线段BH上(如图①)，

此时，AE=tan，FH=tan()，

∴S=S正方形OABH﹣S△OAE﹣S△OHF=1tantan().

②当时，

E在线段BH上，F在线段CH上(如图②)，

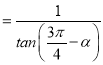此时，EH，FH，可得EF.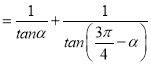

∴S=S△OEF().

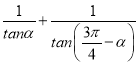综上所述，S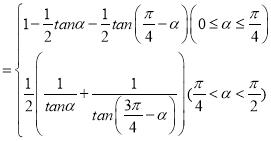

(2)在“一个来回”中，OE共转了2，

其中点G被照到时，共转了2

∴在“一个来回”中，点G被照到的时间为92(分钟).