题目内容
已知函数f(x)=alnx+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数y=f(x)的解析式;
(2)函数g(x)=f(x)+m-ln4,若方程g(x)=0在[ ,2]上恰有两解,求实数m的取值范围.
,2]上恰有两解,求实数m的取值范围.
(1) f(x)=4lnx-x2 ;(2) 2<m≤4-2ln2.
解析试题分析:(1)由切线方程知图像过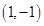 ,求导后,由题可得
,求导后,由题可得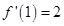 ,分别代函数与导函数表达式,解
,分别代函数与导函数表达式,解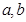 可得;(2)由(1)得g(x)=4lnx-x2+m-ln4,即方程m=x2-4lnx+ln4,在
可得;(2)由(1)得g(x)=4lnx-x2+m-ln4,即方程m=x2-4lnx+ln4,在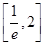 上恰有两解,令
上恰有两解,令
h(x)=x2-4lnx+ln4,由导函数得在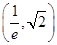 上递减,在(
上递减,在(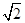 ,2)上递增,可得2< h(x)≤4-2ln2,即2<m≤4-2ln2.
,2)上递增,可得2< h(x)≤4-2ln2,即2<m≤4-2ln2.
解:(1)∵点P(1,f(1))在切线2x-y-3=0上,
∴2-f(1)-3=0,
∴f(1)=-1,故b=-1, 2分
又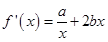 ,∴f ′(1)=a+2b=2,∴a=4,
,∴f ′(1)=a+2b=2,∴a=4,
∴f(x)=4lnx-x2. 4分
(2)g(x)=4lnx-x2+m-ln4
由g(x)=0得:m=x2-4lnx+ln4,此方程在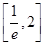 上恰有两解, 6分
上恰有两解, 6分
记h(x)=x2-4lnx+ln4,则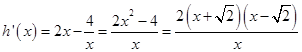 , 8分
, 8分
由h′(x)=0得:x=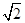 ∈
∈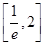 ,
,
在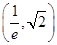 上,h′(x)<0,h(x)单调递减,
上,h′(x)<0,h(x)单调递减,
在(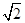 ,2)上,h′(x)>0,h(x)单调递增, 10分
,2)上,h′(x)>0,h(x)单调递增, 10分
又h( )=
)=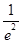 +4+2ln2,h(
+4+2ln2,h(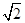 )=2-4ln
)=2-4ln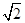 +2ln2=2,
+2ln2=2,
h(2)=4-4ln2+2ln2=4-2ln2,
∵h( )≥h(2),∴2<m≤4-2ln2. 13分
)≥h(2),∴2<m≤4-2ln2. 13分
考点:导数的几何意义,利用导数求函数的值域.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
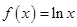 ,
,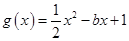 (
(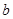 为常数).
为常数).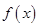 的图象在点
的图象在点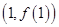 处的切线与函数
处的切线与函数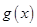 的图象相切,求实数
的图象相切,求实数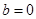 ,
,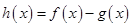 ,
,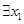 、
、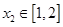 使得
使得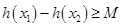 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;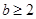 时,若对于区间
时,若对于区间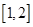 内的任意两个不相等的实数
内的任意两个不相等的实数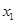 、
、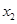 ,都有
,都有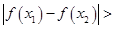
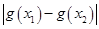 成立,求
成立,求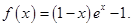
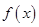 的最大值;
的最大值;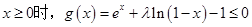 ,求
,求 的取值范围.
的取值范围.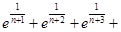 +
+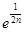
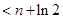 (n
(n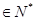 )
)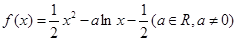 .
.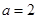 时,求曲线
时,求曲线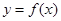 在点
在点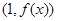 处的切线方程;
处的切线方程;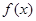 的单调区间;
的单调区间; 都有
都有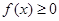 恒成立,求实数
恒成立,求实数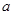 的取值范围.
的取值范围.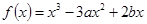 在x=1处有极小值-1,
在x=1处有极小值-1,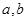 的值; (2)求出
的值; (2)求出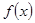 的单调区间.
的单调区间.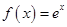 .
.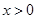 时,设
时,设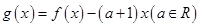 .讨论函数
.讨论函数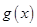 的单调性;
的单调性;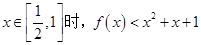 .
.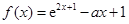 ,
,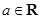 .
.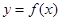 在点
在点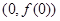 处的切线与直线
处的切线与直线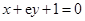 垂直,求
垂直,求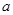 的值;
的值;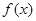 的单调区间;
的单调区间; ,当
,当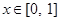 时,都有
时,都有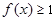 成立,求实数
成立,求实数