题目内容
设函数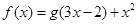 ,函数
,函数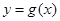 在(1,g(1))处的切线方程是
在(1,g(1))处的切线方程是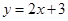 ,则y=
,则y=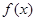 在点(1,f(1))处的切线方程为 。
在点(1,f(1))处的切线方程为 。
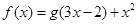 ,函数
,函数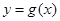 在(1,g(1))处的切线方程是
在(1,g(1))处的切线方程是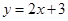 ,则y=
,则y=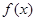 在点(1,f(1))处的切线方程为 。
在点(1,f(1))处的切线方程为 。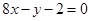
试题分析:把x=1代入y=2x+3,解得y=5,即g(1)=5,由y=2x+3的斜率为2,得到g′(1)=2,∵f′(x)=3g′(3x-2)+2x,∴f′(1)=3g′(1)+2=8,即所求切线的斜率为8,又f(1)=g(1)+1=6,即所求直线与f(x)的切点坐标为(1,6),则所求切线的方程为:y-6=8(x-1),即8x-y-2=0.
点评:此类问题考查了利用导数研究曲线上某地切线方程,要求学生理解切点横坐标代入导函数求出的导函数值为切线方程的斜率,学生在求导时注意g(2x-1)应利用符合函数求导的方法来求.

练习册系列答案
相关题目
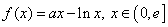 ,其中
,其中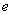 是自然常数,
是自然常数,
 时,
时, 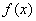 的单调性、极值;
的单调性、极值; ,使
,使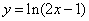 上的点到直线
上的点到直线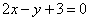 的最短距离是__________.
的最短距离是__________.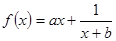 (
(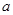 ,b∈Z),曲线
,b∈Z),曲线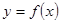 在点(2,
在点(2,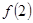 )处的切线方程为
)处的切线方程为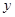 =3.
=3.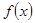 的解析式;
的解析式;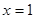 和直线
和直线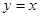 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.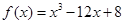 在区间
在区间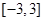 上的最大值与最小值分别为
上的最大值与最小值分别为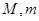 ,则
,则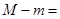 .
.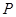 在曲线
在曲线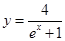 上,
上,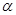 为曲线在点
为曲线在点



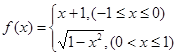 , 则
, 则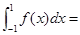 ( )
( )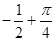
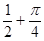
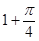
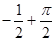
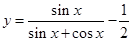 在点M(
在点M(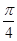 ,0)处的切线的斜率为________________.
,0)处的切线的斜率为________________.