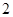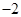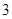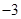题目内容
函数f(x)=x(x-c)2在x=2处有极大值,则常数c的值为________ .
6
试题分析:解:f(x)=x3-2cx2+c2x,f‘(x)=3x2-4cx+c2, f‘(2)=0⇒c=2或c=6.若c=2,f’(x)=3x2-8x+4,令f‘(x)>0⇒x<
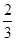 或x>2,f′(x)<0⇒
或x>2,f′(x)<0⇒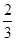 <x<2,故函数在(-∝,
<x<2,故函数在(-∝,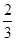 )及(2,+∞)上单调递增,在(
)及(2,+∞)上单调递增,在(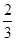 ,2)上单调递减,∴x=2是极小值点.故c=2不合题意,c=6.故答案为6
,2)上单调递减,∴x=2是极小值点.故c=2不合题意,c=6.故答案为6点评:考查学生利用导数研究函数极值的能力,会利用待定系数法求函数解析式.

练习册系列答案
相关题目
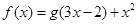 ,函数
,函数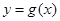 在(1,g(1))处的切线方程是
在(1,g(1))处的切线方程是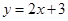 ,则y=
,则y=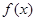 在点(1,f(1))处的切线方程为 。
在点(1,f(1))处的切线方程为 。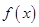 的定义域为
的定义域为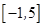 ,部分对应值如表,
,部分对应值如表,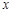
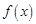
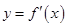 的图象如图所示.
的图象如图所示. 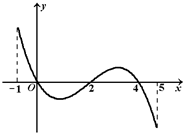
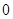 ,
,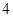 ;
;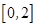 上是减函数;
上是减函数;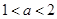 时,函数
时,函数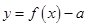 有
有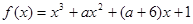 有极大值和极小值,则实数
有极大值和极小值,则实数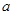 的取值范围是
的取值范围是 或
或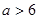
 或
或

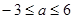
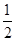 x2-2x在点
x2-2x在点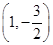 处的切线的倾斜角为( ).
处的切线的倾斜角为( ). ,则
,则 等于
等于 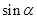



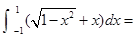 ( )
( )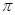
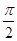
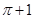
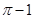
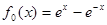 ,且对任意的
,且对任意的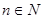 ,都有
,都有 ,则
,则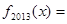
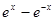
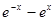
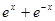
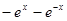
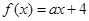 ,若
,若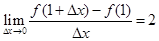 ,则实数
,则实数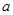 的值为( )
的值为( )