Question

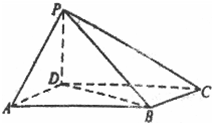如图，四棱锥P-ABCD中，底面ABCD为平行四边形，AB=2AD=2，BD=

3

，PD⊥底面ABCD
（1）证明：AD⊥BD；
（2）若二面角P-BC-D为

π

6

，求AP与平面PBC所成角的正弦值．

Answer 1

分析：（1）利用线面垂直的性质定理证明AD⊥BD．
（2）确定∠PBD即为二面角P-BC-D的平面角，分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系，用坐标表示向量及平面PBC的法向量，利用向量的数量积公式，即可求得AP与平面PBC所成角的正弦值．

解答：解：（1）证明：因为AB=2AD=2，BD=

3

，所以AD=BC=1，CD=AB=2，
∴CD²=BC²+BD²，∴BC⊥BD，
∵底面ABCD为平行四边形，
∴AD⊥BD．
而BC?平面PBC，
∴平面PBC⊥平面PBD…（5分）
（2）∵PD⊥底面ABCD，∴PD⊥BC，
又∵PD∩BD=D，∴BC⊥平面PBD
所以∠PBD即为二面角P-BC-D的平面角，即∠PBD=

π

6

，
而BD=

3

，所以PD=1…（7分）
分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系，则A（1，0，0），B（0，

3

，0），C（-1，

3

，0），P（0，0，1）
所以

AP

=(-1，0，1)，

BC

=(-1，0，0)，

BP

=(0，-

3

，1)，设平面PBC的法向量

n

=(a，b，c)，
则

n ? BC =0 n ? BP =0

，即

a=0 - 3 b+c=0

，可得平面的一个法向量为

n

=(0，1，

3

)．
∴AP与平面PBC所成角的正弦值为sinθ=

| AP ? n |

| AP ?| n ||

=

3

2 2

=

6

4

．…（12分）

点评：本题主要考查线面垂直的性质以及直线与平面所成角的大小的求法，要求熟练掌握空间角的求法．