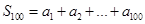题目内容
(本小题满分14分)设数列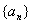 的首项
的首项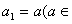 R),且
R),且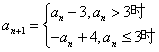 ,
,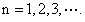 (Ⅰ)若
(Ⅰ)若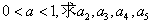 ;(Ⅱ)若
;(Ⅱ)若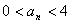 ,证明:
,证明: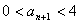 ;(Ⅲ)若
;(Ⅲ)若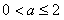 ,求所有的正整数
,求所有的正整数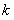 ,使得对于任意
,使得对于任意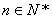 ,均有
,均有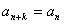 成立.
成立.
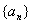 的首项
的首项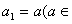 R),且
R),且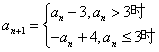 ,
,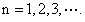 (Ⅰ)若
(Ⅰ)若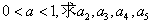 ;(Ⅱ)若
;(Ⅱ)若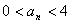 ,证明:
,证明: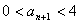 ;(Ⅲ)若
;(Ⅲ)若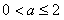 ,求所有的正整数
,求所有的正整数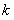 ,使得对于任意
,使得对于任意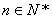 ,均有
,均有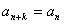 成立.
成立.(1) a2=-a1+4=-a+4,且a2∈(3,4)所以a3=a2-3=-a+1,且a3∈(0,1)所以a4=-a3+4=a+3,且a4∈(3,4)所以a5=a4-3="a"
(2)运用数列的递推关系来分析作差法进行比较证明。
(3)对于参数a要进行分类讨论,然后结合上一问的结论加以证明。
(2)运用数列的递推关系来分析作差法进行比较证明。
(3)对于参数a要进行分类讨论,然后结合上一问的结论加以证明。
试题分析:(Ⅰ)解:因为
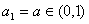
所以a2=-a1+4=-a+4,且a2∈(3,4)所以a3=a2-3=-a+1,且a3∈(0,1)所以a4=-a3+4=a+3,且a4∈(3,4)所以a5=a4-3=a ……4分
(Ⅱ)证明:当
 所以,
所以, ……6分
……6分②当
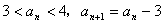 所以,
所以, 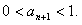 综上,
综上,  ……8分
……8分(Ⅲ)解:①若
 因此,当k=4m(m∈N*)时,对所有的n∈N*,
因此,当k=4m(m∈N*)时,对所有的n∈N*,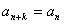 成立 …10分
成立 …10分②若
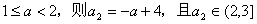
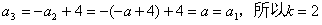 因此,当k=2m(m∈N*)时,对所有的n∈N*,
因此,当k=2m(m∈N*)时,对所有的n∈N*,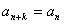 成立 …12分
成立 …12分③若
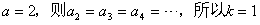 ,因此k=m(m∈N*)时,对所有的n∈N*,
,因此k=m(m∈N*)时,对所有的n∈N*,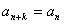 成立 ……13分综上,若0<a<1,则k=4m;
成立 ……13分综上,若0<a<1,则k=4m; ,则k=2m;
,则k=2m;若a=2,则k="m." m∈N* ……14分
点评:该试题主要是涉及到了关于数列与不等式的综合运用,属中档题。

练习册系列答案
相关题目
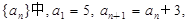 则
则
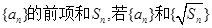 都是等差数列,且公差相等,(1)求
都是等差数列,且公差相等,(1)求 的通项公式;(2)若
的通项公式;(2)若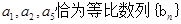 的前三项,记数列
的前三项,记数列 数列
数列 的前n项和为
的前n项和为
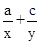 的值;
的值;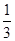 、c="-"
、c="-" 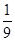 ,试计算
,试计算 中,
中, ,
, ,
, ,则该数列的通项为 。
,则该数列的通项为 。
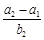 的值是( ).
的值是( ).

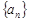 的前 n项和为
的前 n项和为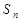 ,满足
,满足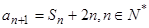 ,且
,且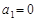 .
.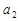 ,
,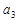 ;
; 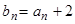 ,求证:数列
,求证:数列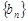 是等比数列。
是等比数列。 , 求数列
, 求数列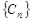 的前n项和
的前n项和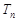 。
。 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为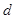 的等差数列;
的等差数列;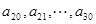 是公差为
是公差为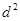 的等差数列(
的等差数列( ).
).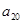 = 30,求
= 30,求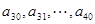 是公差为
是公差为 关于
关于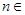 N
N );
); ,试用
,试用