题目内容
二阶矩阵M对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .
.
(Ⅰ)求矩阵M的逆矩阵 ;
;
(Ⅱ)设直线 在变换M作用下得到了直线
在变换M作用下得到了直线 :
: ,求直线
,求直线 的方程.
的方程.
(Ⅰ)  =
= ;(Ⅱ)
;(Ⅱ)  .
.
解析试题分析:(Ⅰ)设 ,则有
,则有 =
=  ,
, =
= ,
,
所以 ,且
,且 ,解得
,解得 所以M=
所以M= ,从而|M|=-2,
,从而|M|=-2,
从而M-1= 。
。
(Ⅱ)因为 =
=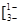 ,且m:2x'-y'=4,所以2(x+2y)-(3x+4y)=4,即x+4=0为直线l的方程。
,且m:2x'-y'=4,所以2(x+2y)-(3x+4y)=4,即x+4=0为直线l的方程。
考点:本题主要考查逆矩阵与投影变换,直线方程等。
点评:中档题,由已知二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).可构造关于a,b,c,d的四元一次方程组,解方程组可得矩阵M,进而得到矩阵M的逆矩阵M-1。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知集合A={x|x2-3x+a>0,x∈R},且1∉A,则实数a的取值范围是( )
| A、(-∞,2] | B、[2,+∞) | C、(-∞,-2] | D、[-2,+∞) |
 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .
. 成立的矩阵
成立的矩阵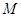 .
.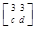 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1=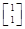 ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2= .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵. ,则
,则 .
. (
( )任意排成
)任意排成 行
行 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行第
行第 列的数(
列的数( ,
,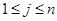 ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________ ,特征值λ2=-1及其对应的一个特征向量α2=
,特征值λ2=-1及其对应的一个特征向量α2= ,求矩阵A的逆矩阵A-1.
,求矩阵A的逆矩阵A-1.