题目内容
(本题满分13分)
已知函数![]() 。
。
(1)若函数![]() 在
在![]() 上是单调递增函数,求实数
上是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 在
在![]() 上的最大值。
上的最大值。
(本题满分13分)
解:![]() (x)=
(x)=![]() +a
+a
(1)只要在x∈[0,2]上![]() (x)≥0恒成立,
(x)≥0恒成立,![]() a≥
a≥![]()
而![]() ∈[
∈[![]() ,1],∴a≥1 (5分)
,1],∴a≥1 (5分)
(2)∵当x∈[0,2]时,![]() ∈[-1,-
∈[-1,-![]() ]
]
∴①当a≤![]() 时,
时,![]() (x)≤0,这时f(x)在[0,2]上单调递减,f(x)≤f(0)=1+ln3
(x)≤0,这时f(x)在[0,2]上单调递减,f(x)≤f(0)=1+ln3
(7分)
②当![]() <a<1时,令
<a<1时,令![]() (x)=0,可解得x=3-
(x)=0,可解得x=3-![]() ,
,
∵当x∈[0,3-![]() ]时,有
]时,有![]() (x)>0
(x)>0
当x∈[3-![]() ,2]时,有
,2]时,有![]() (x)<0,
(x)<0,
∴x=3-![]() 是f(x)在[0,2]上的唯一的极大值,
是f(x)在[0,2]上的唯一的极大值,
则f(x)≤f(3-![]() )=3a-lna (10分)
)=3a-lna (10分)
③当a≥1时,![]() (x)≥0,这时f(x)在[0,2]上单调递增,
(x)≥0,这时f(x)在[0,2]上单调递增,
f(x)≤f(2)=2a+1 (12分)
综上所述: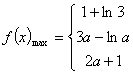
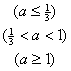 (13分)
(13分)

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.