题目内容
7.在直角坐标系内,O为原点,点A,B坐标分别为(1,0),(0,2),当实数p,q满足$\frac{1}{p}$+$\frac{1}{q}$=1时,若点C,D分别在x轴,y轴上,且$\overrightarrow{OC}$=p$\overrightarrow{OA}$,$\overrightarrow{OD}$=q$\overrightarrow{OB}$,则A线CD恒过一个定点,这个定点的坐标为(1,1).分析 根据向量坐标的定义便可得到C(p,0),D(0,q),从而过C,D的直线方程便为$\frac{x}{p}+\frac{y}{q}=1$,根据条件便可得出点(1,1)满足直线方程,从而点(1,1)在直线CD上,这样便得出了直线CD恒过的定点.
解答 解:根据条件得C点坐标为(p,0),D点坐标为(0,q);
∴过C,D的直线方程为:
$\frac{x}{p}+\frac{y}{q}=1$;
根据条件$\frac{1}{p}+\frac{1}{q}=1$便得点(1,1)满足直线CD的方程;
即直线CD恒过顶点(1,1).
故答案为:(1,1).
点评 考查向量坐标的定义,从坐标原点指向平面上点的向量坐标和该点坐标的关系,向量数乘几何意义,以及直线的截距式方程.

练习册系列答案
相关题目
15.函数f(x)=logax的图象如图所示,则a的取值可能是( )
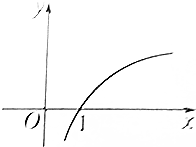
| A. | 10 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |