题目内容
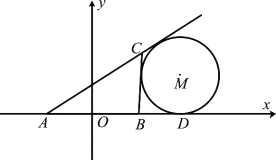
【题目】如图所示,在![]() 中,
中, ![]() 的中点为
的中点为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .固定边
.固定边![]() ,在平面内移动顶点
,在平面内移动顶点![]() ,使得圆
,使得圆![]() 与边
与边![]() ,边
,边![]() 的延长线相切,并始终与
的延长线相切,并始终与![]() 的延长线相切于点
的延长线相切于点![]() ,记顶点
,记顶点![]() 的轨迹为曲线
的轨迹为曲线![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为坐标原点如图所示建立平面直角坐标系.
为坐标原点如图所示建立平面直角坐标系.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】【试题分析】(1)依据题设条件运用椭圆的定义进行分析探求;(2)借助题设条件运用直线与椭圆的位置关系进行分析求解:
(Ⅰ)依题意得![]() ,设动圆
,设动圆![]() 与边
与边![]() 的延长线相切于
的延长线相切于![]() ,与边
,与边![]() 相切于
相切于![]() , 则
, 则![]()
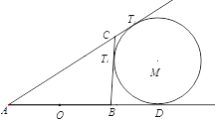
所以![]()
![]() 所以点
所以点![]() 轨迹
轨迹![]() 是以
是以![]() 为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线
为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线![]() 的方程为
的方程为![]() .
.
由于曲线![]() 要挖去长轴两个顶点,所以直线
要挖去长轴两个顶点,所以直线![]() 斜率存在且不为
斜率存在且不为![]() ,所以可设直线
,所以可设直线![]()
由![]() 得
得![]() ,
,![]() ,同理可得:
,同理可得: ![]() ,
,![]() ;
;
所以![]() ,
, ![]()
又![]() ,所以
,所以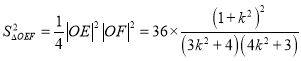 令
令![]() ,
,
则![]() 且
且![]() ,所以
,所以 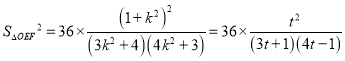
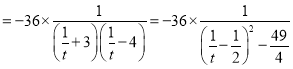 又
又![]() ,所以
,所以![]() ,
,
所以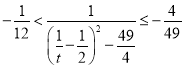 ,
,
所以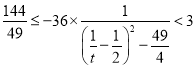 ,所以
,所以![]() ,
,
所以![]() 面积的取值范围为
面积的取值范围为![]() .
.
【法二】
依题意得直线![]() 斜率不为0,且直线
斜率不为0,且直线![]() 不过椭圆的顶点,则可设直线
不过椭圆的顶点,则可设直线![]() :
: ![]() ,且
,且![]() 。
。
设![]() ,又以
,又以![]() 为直径的圆经过点
为直径的圆经过点![]() ,则
,则![]() ,所以
,所以![]()
由![]() 得
得![]() ,则
,则![]()
且![]() ,所以
,所以![]()
又![]()
![]() 代入①得:
代入①得: ![]() ,所以
,所以![]() ,
,
代入②得: ![]() 恒成立所以
恒成立所以![]() 且
且![]() .
.
又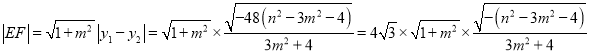 ;
;
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以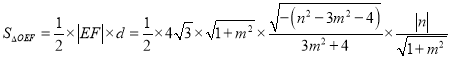
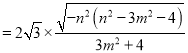
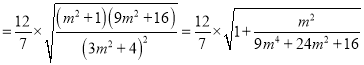
(Ⅰ)当![]() 时,
时, ![]() ;
;
(Ⅱ)当![]() 且
且![]() 时,
时,
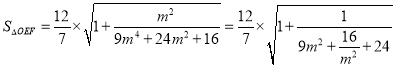 ,
,
又![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”,所以
”,所以![]() ,
,
所以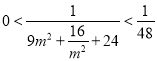 ,所以
,所以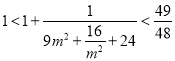 ,
,
所以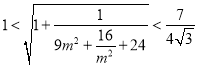 ,所以
,所以![]() ;
;
综合(1),(2)知![]() .
.

练习册系列答案
相关题目