题目内容
已知抛物线C:y2=4x的焦点为F,过点K(-1,0)的直l与C相交于A、B两点,点A关于x轴的对称点为D。 (1)证明:点F在直线BD上;
(2)设 =
= ,求△BDK的内切圆M的方程。
,求△BDK的内切圆M的方程。
(2)设
 =
= ,求△BDK的内切圆M的方程。
,求△BDK的内切圆M的方程。解:(1)设A(x1,y1),B(x2,y2),D(x1,-y1),l的方程为x=my-1(m≠0)
将x=my-1代入y2=4x并整理得y2-4my+4=0
从而y1+y2=4m,y1y2=4 ①
直线BD的方程为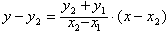
即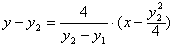
令y=0,得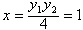
所以点F(1,0)在直线BD上;
(2)由①知,x1+x2=(my1-1)+(my2-1)=4m2-2,x1x2=(my1-1)(my2-1)=1
因为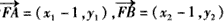
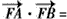 (x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2
(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2
故8-4m2=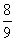 ,解得m=
,解得m=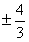
所以l的方程为3x+4y+3=0,3x-4y+3=0
又由①知
故直线BD的斜率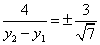
因而直线BD的方程为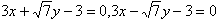
因为KF为∠BKD的平分线,故可设圆心M(t,0)(-1<t<1),M(t,0)到l及BD的距离分别为
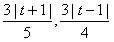 ,由
,由 得
得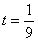 或t=9(舍去)
或t=9(舍去)
故圆M的半径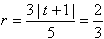
所以圆M的方程为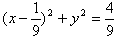 。
。
将x=my-1代入y2=4x并整理得y2-4my+4=0
从而y1+y2=4m,y1y2=4 ①
直线BD的方程为
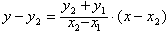
即
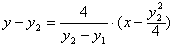
令y=0,得
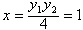
所以点F(1,0)在直线BD上;
(2)由①知,x1+x2=(my1-1)+(my2-1)=4m2-2,x1x2=(my1-1)(my2-1)=1
因为
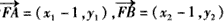
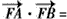 (x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2
(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2故8-4m2=
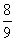 ,解得m=
,解得m=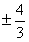
所以l的方程为3x+4y+3=0,3x-4y+3=0
又由①知

故直线BD的斜率
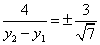
因而直线BD的方程为
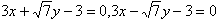
因为KF为∠BKD的平分线,故可设圆心M(t,0)(-1<t<1),M(t,0)到l及BD的距离分别为
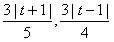 ,由
,由 得
得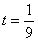 或t=9(舍去)
或t=9(舍去)故圆M的半径
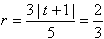
所以圆M的方程为
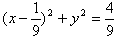 。
。
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.