题目内容
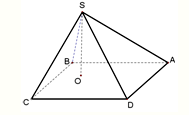在四棱锥S-ABCD中，底面ABCD是边长为a的正方形，顶点S在底面内的射影O在正方形ABCD的内部（不在边上），且SO=λa，λ为常数，设侧面SAB，SBC，SCD，SDA与底面ABCD所成的二面角依次为α1，α2，α3，α4，则下列各式为常数的是①cotα1+cotα2
②cotα1+cotα3
③cotα2+cotα3
④cotα2+cotα4
（ ）
分析：过O点作MN⊥BC，根据二面角的定义易得∠SMO即为侧面SBC与底面ABCD所成的二面角，∠SNO即为侧面SDA与底面ABCD所成的二面角，根据余切函数的定义及SO=λa，λ为常数，易得到答案．
解答：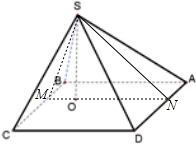
解：过O点作MN⊥BC，则BC⊥AD
则OM，ON分别为BM，BN在底面ABCD上的射影
则∠SMO即为侧面SBC与底面ABCD所成的二面角，∠SNO即为侧面SDA与底面ABCD所成的二面角，
∴∠SMO=α1，∠SNO=α3，
故cotα1=
，cotα3=
则cotα1+cotα3=
+
=
=
=
即cotα1+cotα3为定值
同理可得cotα2+cotα4为定值
故选B
解：过O点作MN⊥BC，则BC⊥AD则OM，ON分别为BM，BN在底面ABCD上的射影
则∠SMO即为侧面SBC与底面ABCD所成的二面角，∠SNO即为侧面SDA与底面ABCD所成的二面角，
∴∠SMO=α1，∠SNO=α3，
故cotα1=
| OM |
| OS |
| ON |
| OS |
则cotα1+cotα3=
| OM |
| OS |
| ON |
| OS |
| MN |
| OS |
| a |
| λa |
| 1 |
| λ |
即cotα1+cotα3为定值
同理可得cotα2+cotα4为定值
故选B
点评：本题以余切函数的定义为载体考查了二面角的定义，其中根据二面角的定义求出二面角的平面角是解答的关键．
练习册系列答案
相关题目
如图，在四棱锥S-ABCD中，AD∥BC且AD⊥CD；平面CSD⊥平面ABCD，CS⊥DS，CS=2AD=2；E为BS的中点，CE=
如图，在四棱锥S-ABCD中，底面ABCD是边长为2的正方形，侧棱SD=2，SA=2
如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是平行四边形，∠BAD=30°，AB=2，
如图所示，在四棱锥S-ABCD中，BA⊥面SAD，CD⊥面SAD，SA⊥SD，且SA=SD=DC=2AB．O为AD中点．
如图，在四棱锥S-ABCD中，SA⊥底面ABCD，∠BAD=∠ABC=90°，BC=3SA=3AB=3AD．