题目内容
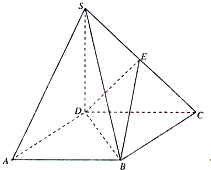 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,AD=
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,AD=| 3 |
(Ⅰ)求证:SA∥平面BDE;
(Ⅱ)求证:AD⊥SB;
(Ⅲ)若SD=2,求棱锥C-BDE的体积.
分析:(Ⅰ)连接AC交BD于F,连接EF,证明SA∥EF,然后证明SA∥平面BDE.
(Ⅱ)利用余弦定理推出AD⊥BD.证明AD⊥SD,然后证明AD⊥SB.
(Ⅲ)若SD=2,求出E到底面的距离,求出底面面积,利用等体积求解求棱锥C-BDE的体积.
(Ⅱ)利用余弦定理推出AD⊥BD.证明AD⊥SD,然后证明AD⊥SB.
(Ⅲ)若SD=2,求出E到底面的距离,求出底面面积,利用等体积求解求棱锥C-BDE的体积.
解答:解:(Ⅰ)连接AC交BD于F,连接EF,由ABCD是平行四边形,知F为AC的中点,
又E为SC的中点,所以SA∥EF,
∵SA?平面BDE,EF?平面BDE,
∴SA∥平面BDE.(4分)
(Ⅱ)由AB=2,AD=
,∠BAD=30°,及余弦定理得
取BD2=AB2+AD2-2AB•ADcos∠BAD=1,
∵AD2+BD2=AB2,∴AD⊥BD.
∵SD⊥平面ABCD,AD?平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SB?平面SBD,
∴AD⊥SB.(8分)
(Ⅲ)SD=2,所以E到底面的距离为1,
S△BCD=
BC•CD•sin∠BCD=
×2×
×
=
,
VC-BDE=VE-BCD=
×
×1=
(12分)
又E为SC的中点,所以SA∥EF,
∵SA?平面BDE,EF?平面BDE,
∴SA∥平面BDE.(4分)
(Ⅱ)由AB=2,AD=
| 3 |
取BD2=AB2+AD2-2AB•ADcos∠BAD=1,
∵AD2+BD2=AB2,∴AD⊥BD.
∵SD⊥平面ABCD,AD?平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SB?平面SBD,
∴AD⊥SB.(8分)
(Ⅲ)SD=2,所以E到底面的距离为1,
S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
VC-BDE=VE-BCD=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
点评:本题考查直线与平面平行,直线与直线垂直直线与平面垂直的应用,几何体的体积的求法,考查计算能力,空间想象能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,