题目内容
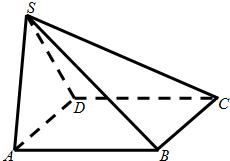 如图,在四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧棱SD=2,SA=2
如图,在四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧棱SD=2,SA=2| 2 |
(1)求证:侧面SDC⊥底面ABCD;
(2)求侧棱SB与底面ABCD所成角的正弦值.
分析:(1)由SD=2,SA=2
,得AD⊥SD,又AD⊥CD,由线面垂直的判定得AD⊥侧面SDC,进而由面面垂直的判定得侧面SDC⊥底面ABCD;
(2)过点S作直线CD的垂线交CD的延长线于点E,由(1)知SE⊥底面ABCD,从而∠SBE是侧棱SB与底面ABCD所成角.
| 2 |
(2)过点S作直线CD的垂线交CD的延长线于点E,由(1)知SE⊥底面ABCD,从而∠SBE是侧棱SB与底面ABCD所成角.
解答:(1)证明:∵SD=2,SA=2
,
∴AD⊥SD,又AD⊥CD,CD?侧面SDC,SD?侧面SDC,
且SD∩CD=D,
∴AD⊥侧面SDC.
又AD?底面ABCD,故侧面SDC⊥底面ABCD.(7分)
(2)解:如图,过点S作直线CD的垂线交CD的延长线于点E,
由(1)可知SE⊥底面ABCD,则∠SBE是侧棱SB与底面ABCD所成角.
∵∠SDC=120°,
∴∠SDE=60°,又SD=2,
故SE=
,DE=1,
则BE=
=
,
故SB=4.
则sin∠SBE=
=
,
故侧棱SB与底面ABCD所成角的正弦值为
.(14分)
| 2 |
∴AD⊥SD,又AD⊥CD,CD?侧面SDC,SD?侧面SDC,
且SD∩CD=D,
∴AD⊥侧面SDC.
又AD?底面ABCD,故侧面SDC⊥底面ABCD.(7分)
(2)解:如图,过点S作直线CD的垂线交CD的延长线于点E,
由(1)可知SE⊥底面ABCD,则∠SBE是侧棱SB与底面ABCD所成角.
∵∠SDC=120°,
∴∠SDE=60°,又SD=2,
故SE=
| 3 |
则BE=
| 32+22 |
| 13 |
故SB=4.
则sin∠SBE=
| SE |
| BE |
| ||
| 4 |
故侧棱SB与底面ABCD所成角的正弦值为
| ||
| 4 |
点评:本题主要考查线面垂直与面面垂直之间的相互转化以及线面角的求法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,