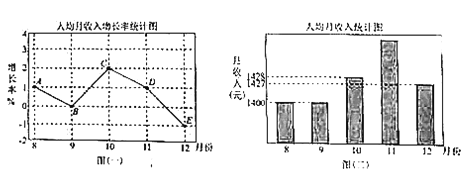
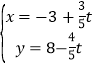��Ŀ����
����Ŀ����ʷ�����еķ�չ������������м�ֵ����ѧ˼�뷽������ʱ���Ľ���������Ҫ�����ã������������ѧ���а��ɶࡤ쳲����������ӷ�ֳΪ�������롰�������С�����1��1��2��3��5��8��13��21��34��55��89��144��233����.��![]() ��
��![]() �����������ִ�����������ṹ����ѧ���������Ź㷺��Ӧ�ã��������б�4���������������һ���µ�����
�����������ִ�����������ṹ����ѧ���������Ź㷺��Ӧ�ã��������б�4���������������һ���µ�����![]() ���ּ�����
���ּ�����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��ֵΪ_____��
��ֵΪ_____��
���𰸡�3
��������
������õ�����![]() ��Ȼ���������
��Ȼ���������![]() �������Կ���ý����
�������Կ���ý����
�ǡ��������С�Ϊ![]() ��������
��������![]() ÿ������4���������������һ���µ�����
ÿ������4���������������һ���µ�����![]() Ϊ
Ϊ![]() ��
��
�ɵ�����![]() ����һ����Ϊ6�����У�
����һ����Ϊ6�����У�
�����������![]() Ϊ
Ϊ![]() ��
��
�۲�����![]() ��֪�Ӹ����дӵ����ʼ�������е����й���һ����Ϊ6�����У���ÿһ���ڵ�������ĺ�Ϊ0��
��֪�Ӹ����дӵ����ʼ�������е����й���һ����Ϊ6�����У���ÿһ���ڵ�������ĺ�Ϊ0��
����![]()
![]() ��
��
�ʴ�Ϊ��3��

��ϰ��ϵ�д�
�����Ŀ