题目内容
(本题满分12分已知函数f(x)=cos(2x-)+2sin(x-)sin(x+).
(1)求函数f(x)的最小正周期; (2)求函数f(x)在区间[-,]上的值域.
解:(1)f(x)=cos (2x-)+2sin(x-)sin(x+)
=cos2x+sin2x+2·(sinx-cosx)·(sinx+cosx)
=cos2x+sin2x-cos2x
=sin2x-cos2x
=sin2xcos-cos2xsin
=sin(2x-). …………………… 4分
∴T==π. …………………… 6分
(2)∵x∈[-,],
∴2x-∈[-,π]. ……………………8分
∵f(x)=sin(2x-)在区间[-,]上单调递增,在区间[,]上单调递减,
∴当x=时,f(x)取得最大值1. ……………………9分
又∵f(-)=-<=f(), ……………………10分
∴当x=-时,f(x)取得最小值-. ……………………11分
∴f(x)的值域为[-,1]. ……………………12分

练习册系列答案
相关题目
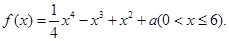
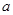 为何值时,方程
为何值时,方程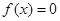 有三个不同的实根.
有三个不同的实根. 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且 .
. ,求数列
,求数列 的前
的前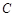 :
: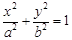 (
(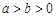 ),其左、右焦点分别为
),其左、右焦点分别为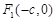 、
、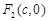 ,且
,且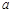 、
、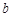 、
、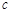 成等比数列.
成等比数列.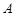 、
、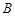 ,求证:
,求证: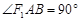 ;
;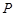 为椭圆
为椭圆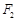 、
、 ,使
,使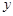 轴的交点
轴的交点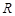 满足
满足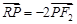 ?若存在,求直线
?若存在,求直线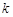 ;若不存在,请说明理由.
;若不存在,请说明理由. 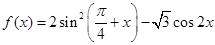 .
. 的最小正周期;
的最小正周期; 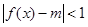 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围 是直线
是直线 上三点,向量
上三点,向量 满足:
满足: ,且函数
,且函数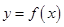 定义域内可导。
定义域内可导。 ,证明:
,证明: ;
; 对
对 及
及 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。