Question

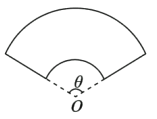
【题目】宜昌一中江南新校区拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米，设小圆弧所在圆的半径为米，圆心角（弧度）.

（1）求关于的函数关系式；

（2）已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米，设花坛的面积与装饰总费用之比为，求关于的函数关系式，并求出的最大值.

Answer 1

【答案】（1），；

（2），的最大值为.

【解析】试题分析：（1）根据扇环的周长等于两段弧长加两段线段，可得，解得，根据题意求自变量取值范围；（2）分别求出花坛的面积与装饰总费用，从而可得关于的函数关系式为，再变量分离，，最后利用基本不等式求最值，注意等于号是否在定义区间.

试题解析：（1）由题可知，所以，.

（2）花坛的面积为（），

装饰总费用为，

所以花坛的面积与装饰总费用之比为.

令，，则，

当且仅当时取等号，此时，.

故花坛的面积与装饰总费用之比为，且的最大值为.