题目内容
已知抛物线y2=2px(p>0)有一内接直角三角形,直角顶点在原点,一直角边的方程是y=2x,斜边长为5
,求此抛物线的方程.
| 13 |
分析:不妨设已知直角三角形为OAB,直线OA的方程为y=2x,由题意可知OA⊥OB,从而有KOB=-
,则可求直线OB的方程,联立方程
可求A的坐标,进而可求AO,同理可求OB,由勾股定理可得,AB2=OA2+OB2,代入可求P,进而可求抛物线的方程
| 1 |
| KOA |
|
解答: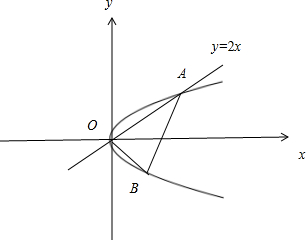 解:不妨设已知直角三角形为OAB,直线OA的方程为y=2x
解:不妨设已知直角三角形为OAB,直线OA的方程为y=2x
∵∠AOB=90°即OA⊥OB,
∴KOB=-
=-
,直线OB的方程为y=-
x
联立方程
可得2x2-px=0
∴xA=
,yA=p
同理可得xB=8p,yB=-4p
∵斜边AB=5
由勾股定理可得,AB2=OA2+OB2=325
∴325=(
)2+p2+64p2+16p2
∵p>0
∴p=2
∴抛物线的方程为y2=4x
 解:不妨设已知直角三角形为OAB,直线OA的方程为y=2x
解:不妨设已知直角三角形为OAB,直线OA的方程为y=2x∵∠AOB=90°即OA⊥OB,
∴KOB=-
| 1 |
| KOA |
| 1 |
| 2 |
| 1 |
| 2 |
联立方程
|
∴xA=
| p |
| 2 |
同理可得xB=8p,yB=-4p
∵斜边AB=5
| 13 |
由勾股定理可得,AB2=OA2+OB2=325
∴325=(
| p |
| 2 |
∵p>0
∴p=2
∴抛物线的方程为y2=4x
点评:本题主要考察了直线与抛物线的相交关系及方程的根与系数的关系的应用,解题中的关键是由直线的垂直关系得到直线OB的斜率.

练习册系列答案
相关题目