题目内容
14.设函数f(x)=min{2$\sqrt{x}$,|x-2|},其中min|a,b|=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$.若函数y=f(x)-m有三个不同的零点x1,x2,x3,则x1+x2+x3的取值范围是( )| A. | (2,6-2$\sqrt{3}$) | B. | (2,$\sqrt{3}$+1) | C. | (4,8-2$\sqrt{3}$) | D. | (0,4-2$\sqrt{3}$) |
分析 先比较2$\sqrt{x}$与|x-2|的大小以确定f(x)的解析式,然后结合函数的图象即可判断符合条件的m的范围,求出x1,x2,x3,的值从而求出x1+x2+x3的取值范围.
解答 解:令y=f(x)-m=0,得:f(x)=m,
由2$\sqrt{x}$≥|x-2|可得x2-8x+4≤0,解可得4-2$\sqrt{3}$≤x≤4+2$\sqrt{3}$,
当4-2$\sqrt{3}$≤x≤4+2$\sqrt{3}$时,2$\sqrt{3}$≥|x-2|,此时f(x)=|x-2|
当x>4+2$\sqrt{3}$或0≤x<4-2时,2$\sqrt{3}$<|x-2|,此时f(x)=2$\sqrt{x}$,
其图象如图所示,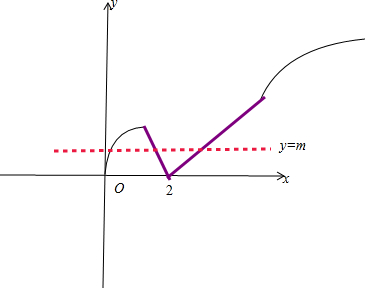 ,
,
∵f(4-2$\sqrt{3}$)=2$\sqrt{3}$-2,
由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2$\sqrt{3}$-2,
不妨设0<x1<x2<2<x3,
则由2$\sqrt{{x}_{1}}$=m得x1=$\frac{{m}^{2}}{4}$,
由|x2-2|=2-x2=m,得x2=2-m,
由|x3-2|=x3-2=m,得x3=m+2,
∴x1+x2+x3=$\frac{{m}^{2}}{4}$+2-m+m+2=$\frac{{m}^{2}}{4}$+4,
当m=0时,$\frac{{m}^{2}}{4}$+4=4,m=2$\sqrt{3}$-2时,$\frac{{m}^{2}}{4}$+4=8-2$\sqrt{3}$,
∴4<x1+x2+x3<8-2$\sqrt{3}$.
故选:C.
点评 本题以新定义为载体,主要考查了函数的交点个数的判断,解题的关键是结合函数的图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.角θ的终边过点P(-1,2),则sinθ=( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
19.下列命题中说法错误的是( )
| A. | 命题“x2-1=0,则x2=1”的逆否命题为“若x≠1,则x2-1≠0”. | |
| B. | “x=1”是“x2=x”成立的充分不必要条件. | |
| C. | 命题“存在x0∈R,2${\;}^{{x}_{0}}$≤0”的否定是“对任意的x∈R,2x>0”. | |
| D. | 若p∩q为假命题,则p,q均为假命题 |