Question

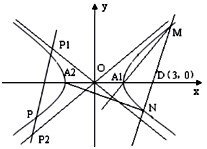（2010•上饶二模）如图，已知P是焦距为上一点，过P的直线与双曲线C的两条渐近线分别交于点P₁，P₂，且

OP

=

1

3

OP1

+

2

3

OP2

，O为坐标原点．
（1）试求当S△OP1P2取得最大值时，双曲线C的方程；
（2）设满足条件（1）的双曲线C的两个顶点为A₁，A₂，直线l过定点D（3，0），且与双曲线交于M，N两点（M不为顶点），求证：直线A₁M，A₂N的交点的横坐标为定值．

Answer 1

分析：（1）先设P（x₀，y₀），P₁（x₁，y₁），P₂（x₂，y₂）．代入

OP

=

1

3

OP1

+

2

3

OP2

，找到坐标之间的关系，再把S△OP1P2用含三点坐标的式子表示，求范围，根据范围找最大值时对应的a，b，即可得到当S△OP1P2取得最大值时，双曲线C的方程．
（2）先设直线l的方程，M，N点坐标，把直线方程代入（1）中所求双曲线C的方程中，求M，N的纵坐标的和与积，再利用两点式求出A₁M，A₂M的方程，联立，求交点，再验证交点横坐标是否为定值．

解答：解：（1）设P（x₀，y₀），P₁（x₁，y₁），P₂（x₂，y₂）．由

OP

=

1

3

OP1

+

2

3

OP2

，得

x0= x1+2x2 3 y0= y1+2y2 3

，
∵点P在双曲线

x2

a2

-

y2

b2

=1上，则

(x1+2x2)2

9a2

-

(y1+2y2)2

9b2

=1
又∵P₁，P₂在渐近线y=±

b

a

x上．
∴x1x2=

9

8

a2，则y1y2=-

9

8

b2S△OP1P2=

1

2

|OP1||OP2|sin∠P1OP2=

1

2

OP1

•

OP2

tan∠P1OP2=

1

2

(x1x2+y1y2)•

2 b a

1- b2 a2

=

1

2

×

9

8

(a2-b2)•

2ab

a2-b2

=

9

8

ab
又a²+b²=c²=8，a²+b²≥2ab，S≤

9

2

．
当且仅当a=b=2时，S有最大值

9

2

．所以双曲线C的方程为：x²-y²=4．
（2）设直线l的方程为x-3=ky，M（x₃，y₃），N（x₄，y₄）．有

x-3=ky x2-y2=4

∴（k²-1）y²+6ky+5=0（k²-1≠0）．
则∴y3+y4=-

6k

k2-1

，y3y4=

5

k2-1

A₁M的方程为y=

y3

x3-2

(x-2)，A2N的方程为 y=

y4

x4+2

(x+2)
直线A₁M，A₂N的交点H的横坐标x_H满足：

y3

x3-2

(xH-2)=

y4

x4+2

(xH+2)
化简得：（x₄y₃+2y₃-x₃y₄+2y₄）x_H=2x₄y₃+4y₃+2x₃y₄-4y₄
即：[2（y₃+y₄）+3（y₃-y₄）]x_H=[4ky₃y₄+6（y₃+y₄）+4（y₃-y₄）][-

12k

k2-1

+3(y3-y4)]xH=4[-

4k

k2-1

+(y3-y4)]∴xH=

4

3

．
故A₁M，A₂N的交点H在直线x=

4

3

．

点评：本题灵活运用了直线与双曲线的关系，求最值，以及判断定植．